Phase shift keying is used to transmit digital data for instance on wireless LAN or RFID technology. The digital information is transmitted by shifting the phase of the carrier signal by a given angle.
see https://en.wikipedia.org/wiki/Phase-shift_keying
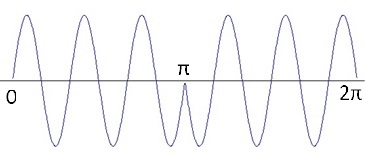
Phase-shift keying signal with 180° phase shift
Phase-shift keying signal with 270° phase shift
Phase-shift keying signal with 90° phase shift
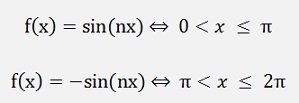
For the bk components:
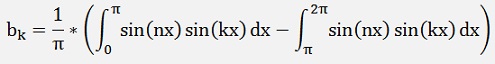
as
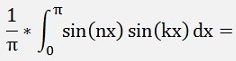
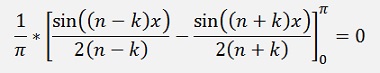
and
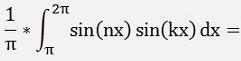
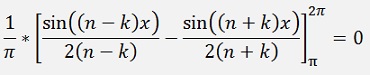
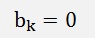
For the ak components
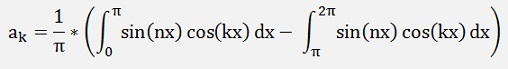
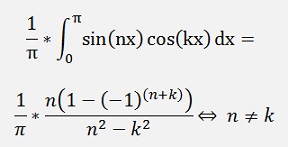
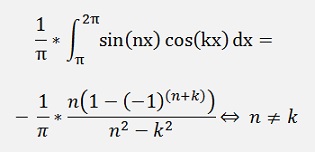
(See ASK signal
 )
)Both put together:
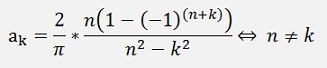
In code with ak as real parts and bk as imaginary parts:
private void Psk180(double peak, int n)
{
int
j;
c[0].real = 0;
for (j = 1; j < 500; j++)
{
}c[0].real = 0;
for (j = 1; j < 500; j++)
{
c[j].imag
= 0;
if ((n + j) % 2 == 0)
c[j].real = 0;
else
{
}if ((n + j) % 2 == 0)
c[j].real = 0;
else
{
if
(j != n)
c[j].real = peak / Math.PI * 4.0 * (double)n / ((double)n * (double)n - (double)j * (double)j);
else
c[j].real = 0;
}c[j].real = peak / Math.PI * 4.0 * (double)n / ((double)n * (double)n - (double)j * (double)j);
else
c[j].real = 0;
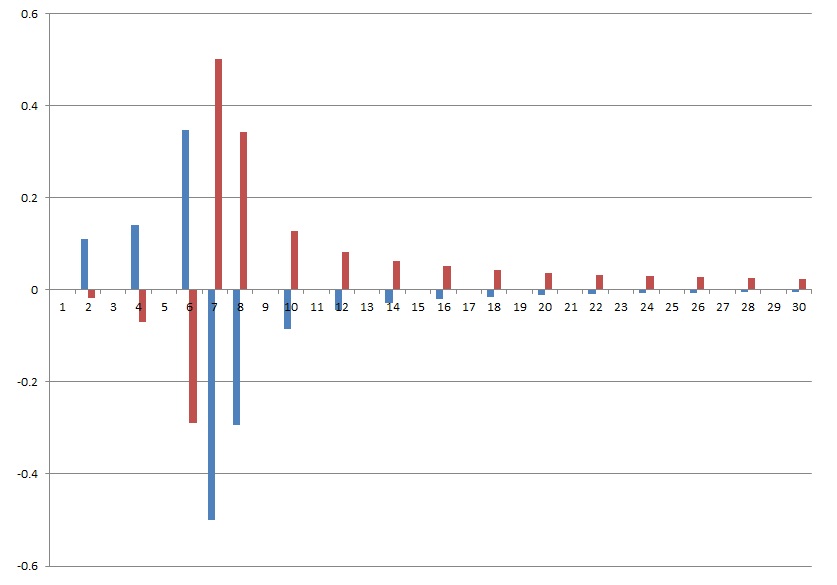
That creates for n=4 a spectrum like:
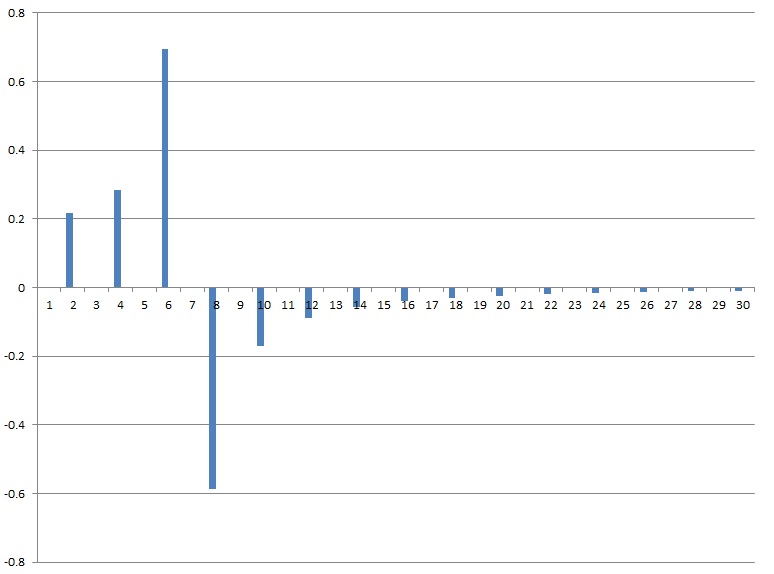
The blue bars are the real elements and red the imaginary parts.
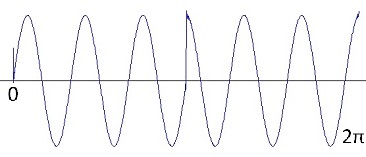
And if all the harmonics are put together, we get the origin signal shape.
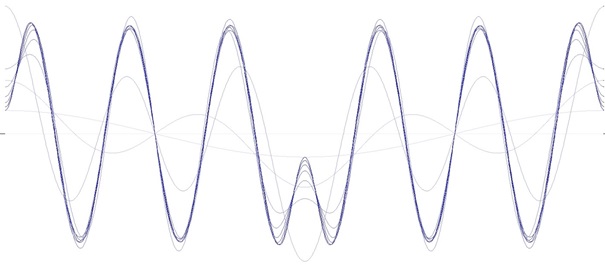
The brightest line is the base frequency. The next darker is the base frequency plus the first harmonic, then comes the same plus the next harmonic … and so on. The more harmonics are included, the closer the shape approximates the origin shape

For a 270° phase shift I combine a sinus signal and a negative cosine signal:
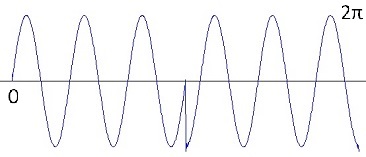
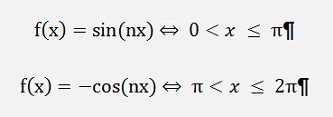
For the bk components
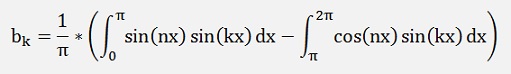
From above
If k <> n
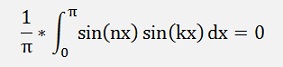
And from the FSK calculations:
If k = n
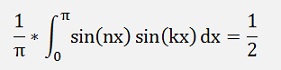
If k <> n
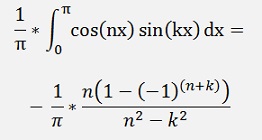
That means
If k = n
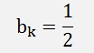
If k <> n and k is odd
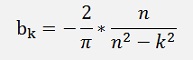
Else bk = 0
For the ak components
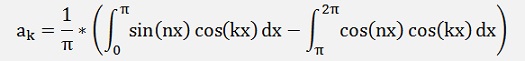
If k <> n
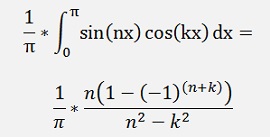
From the FSK calculations:
If k = n
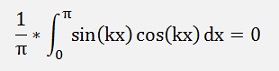
If k <> n
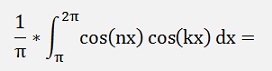
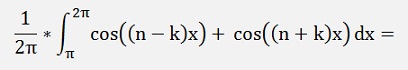
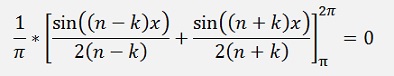
If k = n
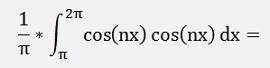
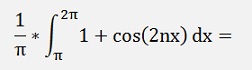
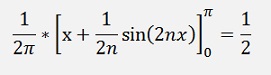
And finally
If k = n
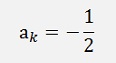
If k <> n and k is odd
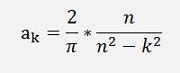
Else ak = 0
This put into a c# function
private
void Psk270(double
peak, int n)
{
{
int
j;
c[0].real = 0;
for (j = 1; j < 500; j++)
{
}c[0].real = 0;
for (j = 1; j < 500; j++)
{
c[j].imag
= 0;
{
}{
if
(j != n)
{
else
{
}{
if
((n + j) % 2 == 0)
{
else
{
}{
c[j].real
= 0;
c[j].imag = 0;
}c[j].imag = 0;
else
{
c[j].real
= peak / 3.141596 * 2.0 * (double)n
/ ((double)n * (double)n
- (double)j * (double)j);
c[j].imag = -peak / 3.141596 * 2.0 * (double)j / ((double)n * (double)n - (double)j * (double)j);
}c[j].imag = -peak / 3.141596 * 2.0 * (double)j / ((double)n * (double)n - (double)j * (double)j);
else
{
c[j].real
= -peak * 0.5;
c[j].imag = peak * 0.5;
}c[j].imag = peak * 0.5;
And that creates the following spectrum
Phase-shift keying signal with 90° phase shift
and
If k = n

If k <> n and k is odd

That changes the look of the spectrum one more time
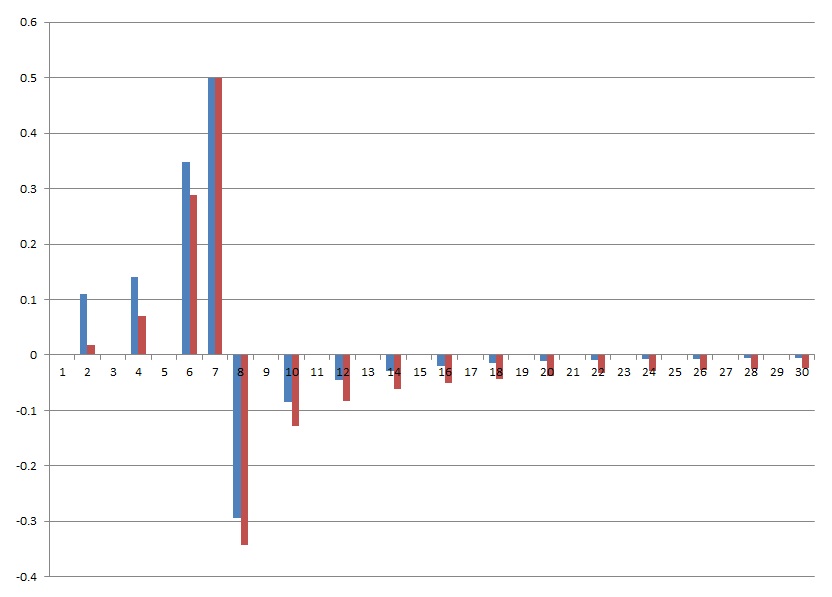
C# Demo Project Fourier signals

