The Boltzmann machine is basically an extension of the Hopfield network (see https://en.wikipedia.org/wiki/Hopfield_network). In the simplest form the Boltzmann machine can be described as a special kind of a neural net with just one layer where each knot of this layer has a bidirectional link wij to each other knot and an offset bj. Each knot represents one input feature and is at the same time output of the net. In a graphic for 5 features that would look like:
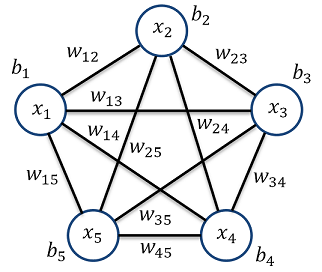
The Hopfield network, as well as the Boltzmann machine, both are capable to reconstruct patterns. If they are trained with some patterns and later on fed with a pattern that is slightly corrupted or has some anomaly, the Hopfield network or Boltzmann machine can find the pattern that is best fitting and reconstruct the corrupted one. The Hopfield network is quite a simple approach, but it has its limits whereas the Boltzmann machine is rather complicate but much more powerful.
In the Hopfield network the calculations are quite simple. For each knot there is a sum
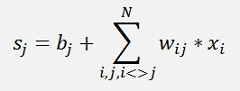
And if this sum is positive, the knots output is 1 else its -1 and as the output is the same as the input xj, we have:
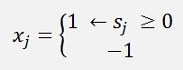
In the Boltzmann machine we have the same sum but this sum is fed into the sigmoid function as activation:
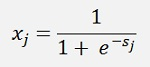
That makes the output of the Boltzmann machine a probability which is much more sensitive than just 1 or -1 of the Hopfield network

Now with each calculation of xj there is not just an output computed but also the input manipulated. That means if I compute a xk, compute xj and compute xk again, I’ll get different results for xk. At least in the beginning it will be so. If I do the same for several times the difference will become smaller each time and after a certain number or repetitions the difference will be 0. That’s when a stable state in the network is reached.
The Hopfield network and the Boltzmann machine both are so called energy based models. In the literature there is usually an energy function mentioned
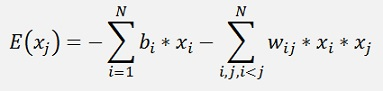
And if the stable state is reached this energy is at its minimum called equilibrium.
Training of the Boltzmann machine
According to the Boltzmann distribution the probability distribution of the x is
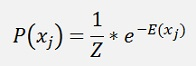
This formula looks so simple but in fact it’s rather complicate. In the Boltzmann machine in the second part
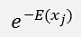
The energy is computed by the model distribution. That’s the distribution of x computed by the actually learned wji and bj parameters. Therefore I marked xj like:
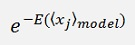
with

For Z the wji, bj and xi parameters of the equilibrium should be used.
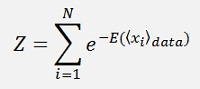
with
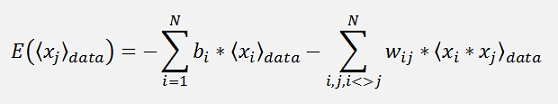
The xi parameters of the equilibrium are the input values of the data used for the training. But the wji and bj parameters of the equilibrium are searched and we don’t have them jet. So for the wji and bj the actually trained data is used.
The probability P(xj) of the Boltzmann distribution shall be maximized which is equal to minimize the negative probability
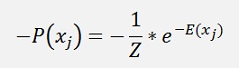
Therefore the logarithm of both sides of the equation is built as this operation does not change the location of the minimum but makes the mathematics much easier.
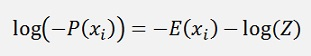
Now the minimum of -P(xj) is there where its derivation is 0. For this derivation the function can be split in 2 parts:
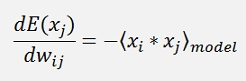
and
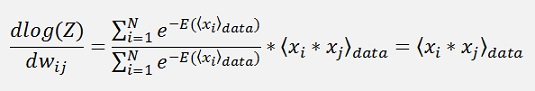
and with this
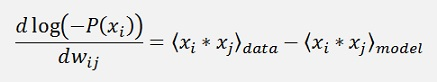
For bi it’s almost the same:
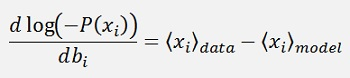
And for the gradient descend:
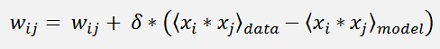
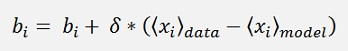
With δ as the learning rate.
At the end it is quite simple:
In a loop for each training sample and each xi of this sample we have to compute one xi, select another xj out of the computed (or just initialized) model data, fetch the corresponding xi and xj from the training data and subtract the multiplication of both model values from the multiplication of the training data values. This multiplied by a small learning rate must be added to the corresponding actual learned wij and the similar is done with bi.
This sequence must be repeated till all wij and bi values remain stable.
In a C# sequence that would look like:
int i, j, k, l;
double[] x_ori = new double[features];
double[] x = new double[features];
double tempW;
int count = 0;
double change = 1000;
while ((change > 2.5E-5) && (count < maxNumberOfCicles))
{
count++;
change = 0;
for (k = 0; k < data.values.Count; k++)
{
for (i = 0; i < features; i++)
{
x[i] = data.values.ElementAt(k)[i];
x_ori[i] = data.values.ElementAt(k)[i];
}
for (i = 0; i < features; i++)
{
tempW = b[i];
for (j = 0; j < features; j++)
{
if (j != i)
tempW = tempW + w[i, j] * x[j];
}
x[i] = 1.0 / (1.0 + Math.Exp(tempW));
}
for (i = 0; i < features; i++)
{
b[i] = b[i] - learningRate * (x_ori[i] - x[i]);
for (j = 0; j < i; j++)
{
if (i != j)
{
w[i, j] = w[i, j] - learningRate * (x_ori[i] * x_ori[j] - x[i] * x[j]);
w[j, i] = w[i, j];
change += learningRate * (x_ori[i] * x_ori[j] - x[i] * x[j]) * learningRate * (x_ori[i] * x_ori[j] - x[i] * x[j]);
}
}
}
}
}
There is a small speed improvement in this sequence: As the matrix W is symmetric, we don’t have to calculate all wij elements. It’s sufficient to calculate the wij elements above the main diagonal of the matrix. That means the elements where j < i. The elements below the main diagonal can be copied from the elements above with
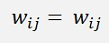
That reduces the calculation time by 20 %. O.k. that’s not too much, but better than nothing

To check if all wij and bi values are stable I just check the wij values. That’s enough. As long as bi changes, wij changes as well and if wij is stable, bi must be stable to.
With these learned parameters the Boltzmann machine is applied with the formula:
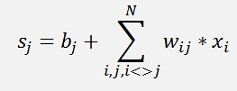
and

This again must be done in a loop running until all xj are stable.
That looks like:
public void calculateOutput(double[] x)
{
int i, j, count;
double tempE;
double tempX;
double change = 100;
count = 0;
while((change > 1E-10) && (count < 200))
{
change = 0;
count++;
for (i = 0; i < features; i++)
{
tempE = b[i];
for (j = 0; j < features; j++)
{
tempE += w[i, j] * x[j];
}
tempX = 1.0 / (1.0 + Math.Exp(tempE));
change += (x[i] - tempX)* (x[i] - tempX);
x[i] = 1.0 / (1.0 + Math.Exp(tempE));
}
}
}
get’s the input in the array x and puts the output into the same array.
Demo Project
My demo project identifies numbers 0 to 9 scanned from a picture and uses the Boltzmann machine to rebuild these numbers after scanning and scaling them down to a fixed size.
A scanned and scaled number can look like:
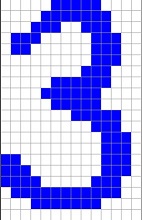

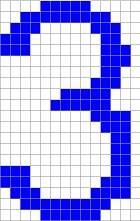
and should be recognized as a 3. Therefore the Boltzmann machine is used to recreate the correct shape of a scanned number and make a

out of these 3 different shapes. This rebuilt shape can be compared to the reference shape of the learned numbers.
The reference character set I use is:
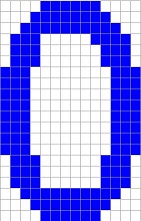
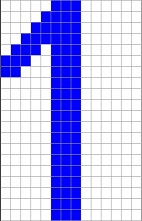


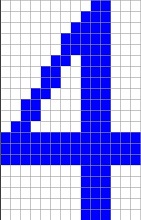
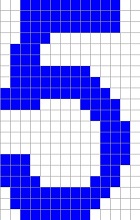
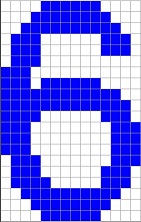
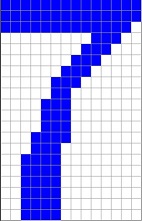
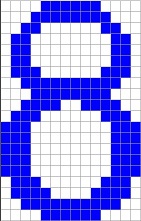
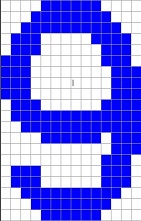
It is stored in the file Characterset.csv and it is basically taken from the Arial character set. I use a character size of 14*20 pixels. So, if some numbers should be recognized, they should look Arial like with 14*20 pixels. I tried some hand written numbers and they were recognized correct. But I had to write them really Arial like. Otherwise it might not work. If some different shapes should be recognized, the algorithm must be trained with these shapes.
There is one point to remark: The number 7 is a bit wider in the lower part than the original. I had to make it wider to be able to work with skewed images.
I implemented 2 C# demo projects: The first one:
“Boltzmann_14_20.zip” is the application to train the Boltzmann machine. It loads the reference character set from Characterset.csv, trains the Boltzmann machine and stores the trained wij a bi parameters in the json file trained.json.
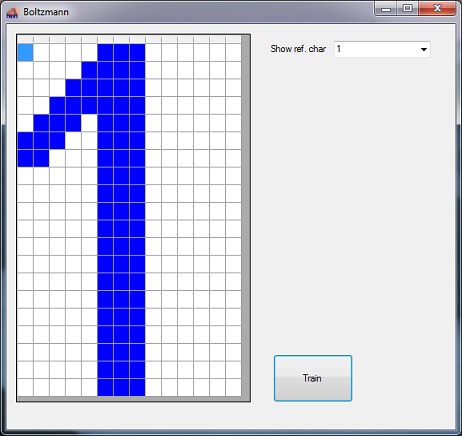
Boltzmann training application
This json file must be copied to the second project:
“Boltzmann_14_20_Test.zip”. In this application a png image file containing the numbers to detect can be loaded and scanned.
A class ImageProcessor scans the image from left to right from top to bottom, detects pixels that belong to the numbers, collects them in a set of lists containing one character in each set, then it scales down the size of the characters to 14*20 pixel and writes these rescaled characters into an array that can be fed into the Boltzmann algorithm. Then one by one, the shape of the characters are recreated by the Boltzmann machine. The recreated characters finally will be compared to the reference characters. That’s roughly the mechanism.
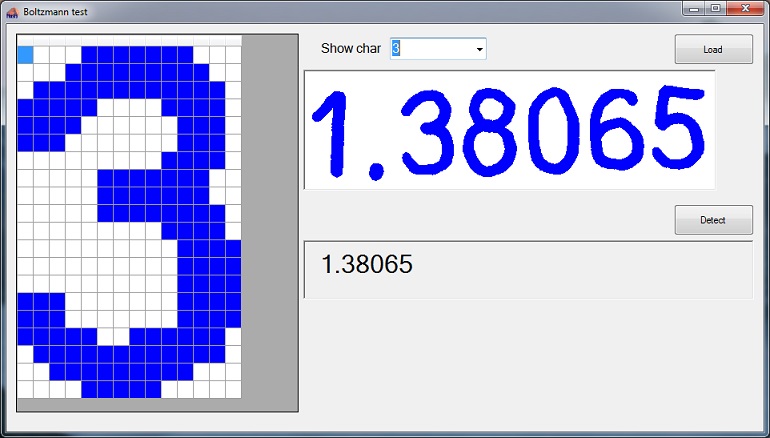
Boltzmann test application
Detailed description
The loading of the image file is not a big deal. There is just one thing to mention: The image should not be too big and there should be a reasonable difference between the brightness of the background colour and the foreground colour.In the function FindChars(Bitmap img) the loaded image is scanned for pixels that differ in the brightness from the background. Pixels differing enough in the brightness I add to lists of pixel-groups belonging together. Pixels that are closer than a minimum distance of 6 pixels I put into the same list by the function AddPoint(Point p). The scanning goes like:
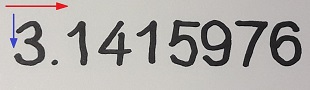
In an outer loop I run from left to write and in the inner loop from top to bottom as marked by the red and blue arrow. After this scanning I have the numbers separated in lists. But there is the situation, that the numbers 2, 3, 5 and 7 are split into more than one list like
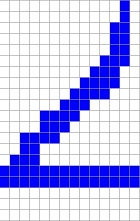
These lists must be joined in the function JoinLists(). After this all numbers are collected in the object array
public STChars[] character;
The class STChars contains a list of the scanned coordinates of one character, the integer array charReseized which is the array that can be processed by the Boltzmann machine and there is a flag isComma. I use this isComma to mark a decimal point. I first had the decimal point in my reference character set and trained the Boltzmann machine with it. That did not work. With this decimal point included the Boltzmann machine was no more capable to recognize the number 7. That’s a weakness of the Boltzmann machine. It cannot deal with every kind of patterns.
So another solution was required. Now while rescaling I check the size of a character in vertical direction and if this is smaller than 1/3 of the maximum size of the characters, I say that’s a decimal point and mark that in the flag isComma.
The resizing in the function Resize(int iWidth, int iHeight) scales a scanned character down. An increasing of the size of a scaled character is not implemented. So the scanned character must be bigger than or at least of the size 14 x 20 pixels. That’s an important limitation. The resizing is implemented quite simple. I take 2 x 2 or 3 x 3 pixels and make one of them. If the characters of the scanned image are much bigger than 14 x 20 pixels it could be advisable to rescale the image first by a .NET resize function. The resized image is written into the charReseized array and this array is fed into the Boltzmann machine finally. An important fact is that this array will contain the rebuilt character afterwards.
Finally I compare each found character to each character of the reference set and if they are equal, I detected one character

In the test application there are 5 .png sample images. 4 of them I took with my mobile phone. With these the algorithm works fine and it should be able to deal with other images as well.
The Boltzmann machine is quite a cool algorithm with a formulation out of the gas thermodynamics. That's really fascinating. But it is somewhat resources consuming. In this implementation with 14*20 bit characters it computes an array of 240x240 wji parameters and 240 bj parameters. That’s 78680 parameters and that just to recognize 10 different numbers. That’s quite an effort


