To implement a linear regression algorithm in an iterative form does not make too much sense as there is a classic algorithm that calculates this at once (see Linear regression) but never the less it is a good way to understand the gradient descent algorithm which is used in machine learning algorithms.
The linear regression approximates a random number of supporting points (x,y) to a straight line with the formulation

with the offset as the place where the line crosses the cero line of x and the rise the direction of the line. The placement of the line is optimized the way that the sum of the square of the deviation to the supporting points is smallest as possible.
For an iterative approach the idea is to search the offset and rise for which the mean of the deviations in square becomes the smallest. That means

A square function has a quite a simple minimum like:
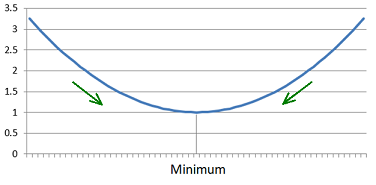
To approach this minimum from the left side we have to move towards right. To approach from the right side we have to move towards left. Mathematical said that means. If the differential is > 0 we have to move to smaller x and if the differential is < 0 we have to move to bigger x. With other words: The differential must be taken into account negative.
Now the differentiation of the above function with respect to the rise is:

that can as well be written as

The differentiation of
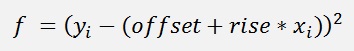
is:

With this differentiation for the sum of all supporting points a rise is computed by the use of all supporting points like

As mentioned above, this rise’ must be taken into account negative to move towards the minimum. That means we have to start at a certain point (that means with a certain rise). Calculate the rise’ at this point and with this rise’ and a small fixed factor, the so called learning rate, the actual rise is adjusted:

The value of rise’ is basically used to set the direction. If the slope is steep, the value of rise’ is big to. To avoid an overshoot in such a situation the learning rate is used. With this the step is kept small enough, that there can no overshoot happen.
In a C# function that’s:
double update_rise(double[] x, double[] y, double rise, double offs, double learning_rate)
{
double rise_deriv = 0;
for (int i = 0; i < samples; i++)
{
// Calculate partial derivative
rise_deriv += -2 * x[i] * (y[i] - (rise * x[i] + offs));
}
rise -= (rise_deriv / samples) * learning_rate;
return rise;
}
The adjusting value is subtracted from the actual rise value because we are searching for the minimum and want to move downward the slope.
With this new rise the mean deviation square is computed. This deviation is often called cost and the function that computes it is the cost function

Or in a c# function:
double cost_function(double[] x, double[] y, double weight, double bias)
{
double cost = 0.0;
for (int i = 0; i < samples; i++)
{
return cost / samples;
}for (int i = 0; i < samples; i++)
{
cost += (y[i] - (weight * x[i] + bias)) *
(y[i] - (weight * x[i] + bias));
}return cost / samples;
If this 2 operations are called iteratively, the deviation, or cost, will decrease slowly till it gets to a minimum. And as at the minimum the derivation is 0, the change will be 0 there too, at least ideally. In reality there can be an overshoot. The minimum that will be found will most probably not be the absolute minimum. There is still the offset that might not fit.
In the literature I found articles that say you have to derive the deviation function for the offset as well and calculate

and

And for this they use the same learning rate as is used to adjust the rise. So they compute the rise and offset at once.
I implemented the algorithm according to this formulation and tried it. The algorithm converged and it returned a result. But at a first trial this result was absolutely wrong. I stopped the iteration after 100 loops. That was much too few. It took 200 000 iterations to get the correct result. That’s quite a lot, makes the algorithm quite slow and takes a lot of calculation effort.
I tried a bit a different approach and treat the offset separately in my implementation. With a starting offset of 0 I compute the rise for the smallest deviation square. As the offset is most probably not correct, there will be a big deviation square. The mean of the deviation (not in square) is big as well. This mean deviation is quite well related to the offset. The closer the offset gets, the smaller the mean deviation will be. Therefore my idea was just to correct the offset by the mean deviation and repeat the search for the best approximation. If this sequence is repeated in a loop, the mean deviation will decrease and the offset gets closer and closer and finally converges to the correct offset.
With this approach it takes 43 iterations to get the correct offset and for each iteration there are 9 iterations to compute the rise. That makes 400 iterations to get the same result as with the 200 000 iterations further above.
The Gradient Descend converges quite slow and tends to oscillate. Computing the offset separately improves this behaviour quite a bit

In a C# function that's:
double find_min(double[] x, double[] y, double rise, double offs, double learning_rate, int maxIers)
{
{
int count = 0;
double oldCost = -1;
double divCost = oldCost - cost;
while(Math.Abs(divCost) > 1e-5 && count < maxIers)
{
return rise;
}double oldCost = -1;
double divCost = oldCost - cost;
while(Math.Abs(divCost) > 1e-5 && count < maxIers)
{
rise = update_rise(x, y, rise, offs,
learning_rate);
cost = cost_function(x, y, rise, offs);
divCost = oldCost - cost;
oldCost = cost;
count++;
if (divCost < -0.001)
{
}cost = cost_function(x, y, rise, offs);
divCost = oldCost - cost;
oldCost = cost;
count++;
if (divCost < -0.001)
{
learning_rate = -learning_rate / 2;
}return rise;
And the complete linear regression:
private void linear_regression()
{
int count = 0;
double oldCost = 1e60;
double divCost = 10;
double offset_step = 0.1;
offset = 0;
rise = startRise;
while ((Math.Abs(divCost) > 0.00002) && (count < 1000))
{
rise = find_min(xp, yp, rise, offset, learning_rate, iterations);
divCost = oldCost - cost;
if (divCost < -0.001)
{
offset_step = -offset_step / 2.0;
}
oldCost = cost;
count++;
offset = offset + mean_function(xp, yp, rise, offset);
}
}
with
double mean_function(double[] x, double[] y, double weight, double offset)
{
double mean = 0.0;
for (int i = 0; i < samples; i++)
{
mean += y[i] - (weight * x[i] + offset);
}
return mean / samples;
}
With this implementation I get for my sample values

The offset = 8.475 and rise = 0.2261. That makes a mean deviation of 22.6.
The same data in the classic linear regression gives an offset = 8.4676 and rise = 0.2263. That’s quite close

Of course this implementation is set up for this sample data now. For other data the learning rate, offset step and starting values for rise and offset might have to be changed. In general the more data samples are there the smaller the learning rate should be chosen.
The big point to remember is the fact that an offset must be treated separately from a rise function. This is valid for rise functions of higher complexity as well and will be used in Gradient Descend

