This article is based on logistic gradient descend. A detailed description of this algorithm can be found on Logistic Regression
If the amount of data, that should be processed by the gradient descent algorithm, is very big, the data processing becomes very time consuming and the accuracy of the approximation can suffer. To avoid this, a mini batch gradient descent algorithm can be applied for the optimisation. The mini batch gradient descend algorithm is basically the same as a normal gradient descend algorithm. It only uses not the entire data set to compute one loop but a small subset of random selected data samples. With these samples it calculates the gradient for one loop.
The gain of this approach is that, with a large amount of data, the algorithm can converge and find the minimum deviation without having to process the complete data set. That can save quite some time.
But of course there is also a price to be paid for this reduction of calculation time. The algorithm uses for each loop another subset of the data. Each of these subsets has its minimum deviation on a little different place compared to the other subsets. That means the target, where the algorithm aims to, moves a little bit each loop. It does not slide away, but it jumps around with very little jumps. That brings some kind of noise into the algorithm which affects it on many places. The cost jumps and with it the change of the cost from one loop to the next. The values for the rise and offset tend even more to oscillate and the maximum reached accuracy will be lower because of this jumping. The cost function in a gradient descend algorithm usually looks like:
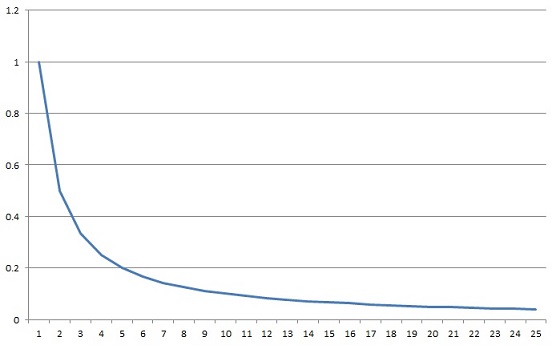
In a mini batch gradient descend it can look like:
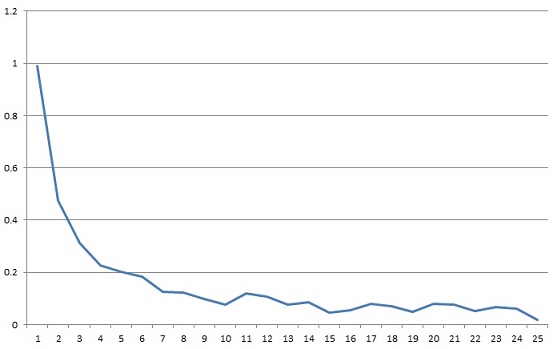
Every small peak is a local maximum and every small minimum is a local minimum. That makes it rather difficult to find a useful stop criterion. Another essential result of this effect is that the result of the optimisation will be different from one run to another. As there are random samples selected for each mini batch, there will always be different batches used and due to that different results will be found. The difference is not too big, but the result of the algorithm is therefore not 100% reproducible.
The smaller the mini batch is the bigger are these effects. One solution to avoid these problems at least partly is to select as big mini batches as possible. But big mini batches result in long calculation time. That’s a bit a dilemma

Another solution is to use a so called momentum to compute the update values for the rise values. The update of the rise values can be regarded as a speed at which the algorithm approaches its target. This speed jumps around because of the mini batch. The momentum is a smoothing of this speed which brings more ease into the algorithm. The momentum keeps a history of the speed and adds only a part of a newly computed speed value to this history like

So there is a history of all computed speed values kept and the older a speed value is the smaller its weight is. That’s the idea of the momentum.
I implemented the logistic regression algorithm processing the Iris data set (once again
 ) with these modifications and there now the
function to compute the rise and offset looks like:
) with these modifications and there now the
function to compute the rise and offset looks like:
double[] update_rise(Collection<double[]> values, double[] rise, double learning_rate)
{
int i, j;
double k = 2; // momentum factor
double[] d_rise = new double[features_out];
double[] x;
double y;
double e;
double[] tempSum = new double[2];
double tempValue;
for (i = 0; i < features_in; i++)
{
d_rise[2 * i] = 0;
d_rise[2 * i + 1] = 0;
tempSum[0] = 0;
tempSum[1] = 0;
for (j = 0; j < values.Count; j++)
{
x = values.ElementAt(j);
y = x[features_in];
e = Math.Exp(F_x(x, rise, offset));
tempValue = 2.0 * x[i] * e / (1.0 + e) / (1.0 + e) * (y - 1.0 / (1.0 + 1 / e));
tempSum[0] = tempSum[0] - x[i] * tempValue;
tempSum[1] = tempSum[1] - tempValue;
if (Math.Abs(tempSum[0]) > 1e6)
{
d_rise[2*i] = d_rise[2*i] + tempSum[0] / values.Count;
tempSum[0] = 0;
}
if (Math.Abs(tempSum[1]) > 1e6)
{
d_rise[2*i+1] = d_rise[2*i+1] + tempSum[1] / values.Count;
tempSum[1] = 0;
}
}
d_rise[2 * i] = d_rise[2 * i] + tempSum[0] / values.Count;
d_rise[2 * i+1] = d_rise[2 * i+1] + tempSum[1] / values.Count;
}
for (i = 0; i < features_out; i++)
{
// update rise by the use of the momentum
momentum[i] = (k * momentum[i] + learning_rate * d_rise[i]) / (k + 1);
rise[i] = rise[i] - momentum[i];
}
return rise;
}
And it is called with the mini batch in the function find_min:.
double[] find_min(Collection<double[]> values, double[] rise, double learning_rate, int maxIers)
{
int i;
int count = 0;
int actIndex;
double oldCost = 100000;
double divCost = oldCost - cost;
double[] ret = new double[2];
Collection<double[]> batch = new Collection<double[]>();
Random rnd = new Random();
while (Math.Abs(divCost) > 1.0e-12 && count < maxIers)
{
batch.Clear();
for (i = 0; i < batchSize; i++)
{
actIndex = rnd.Next(1, samples - 1);
batch.Add(values.ElementAt(actIndex));
}
rise = update_rise(batch, rise, learning_rate);
cost = cost_function(values, rise);
divCost = oldCost - cost;
oldCost = cost;
count++;
}
return rise;
}
For the outer loop I had to make a small modification to. As the cost function can still jump around a little, it can be that the loop never reaches the situation that the change of the cost function is small enough for the algorithm to stop. Therefore I add the stop criterion to stop if the step that adds to the offset is small enough. With this the main loop looks like:
while ((Math.Abs(divCost) > 1.0e-6) && (Math.Abs(step) > 0.03) && (count < maxLoops))
{
rise = find_min(data.values, rise, learning_rate, maxIterations);
divCost = oldCost - cost;
if (divCost < -1.0e-5)
{
step = -step / 2.0;
}
lastCost = oldCost;
oldCost = cost;
offset = offset - step;
count++;
}
And with these modifications I got the parameters:
Iris Versicolor
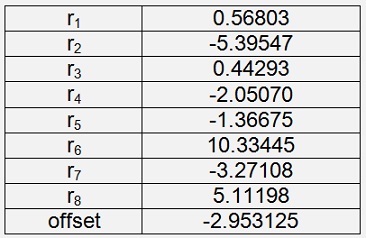
With a cost of 0.0112
Iris Setosa
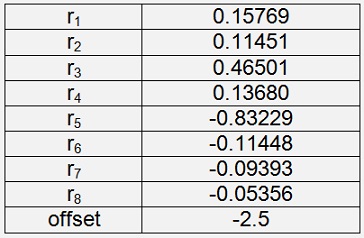
With a cost of 2.21E-05
Iris Virginica
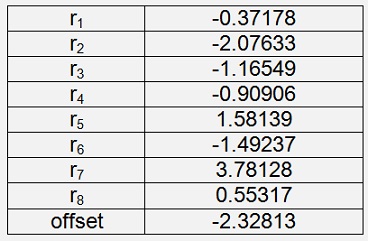
With a cost of 0.0067
Same as for the other algorithms processing the Iris data set I split the data set into 135 samples for training and 5 samples of each class for testing. The test application recognises all 15 samples correct with a mean probability of 98%. Compared with the Logistic Regression implementation it is not too much faster. But the algorithm is not meant to deal with such small data sets and if it is used with around 100000 data samples and a mini batch size of 200, the gain will be quite a bit bigger


