Many mathematical problems cannot be solved by using “only” real numbers. The prime example for such a problem is the root of a negative number. This root does not exist for a real number. That might sound simple and not requiring some other kinds of numbers just to see what solution the root of a negative number has. But there are more interesting problems requiring complex numbers

Complex numbers are basically 2 dimensional numbers and they are an extension of real numbers as they consist of the real part and an imaginary part. The imaginary part is vertical to the real part.
A complex number can by written in two forms:
In the Cartesian form the complex number is written like a point in a XY-field. It has two coordinates. One is the real part and the other one is the imaginary part, which is marked by an “i” or “j” (depending where you study). The “i” can be on the left side or the wright side of the imaginary number like
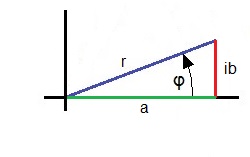
This complex number has an absolute size which is the length of beam given by a and b. That means
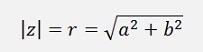
and it has an angle φ given by a and b:
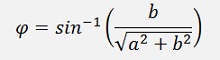
The angle is always counter clockwise and is never negative. If the imaginary part is negative, the angle is bigger than PI.
In the polar form the complex number is expressed by just its length and angle. Often Euler's formula is used. There the angle is written as e to the power of iφ.
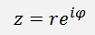
The conjugate complex to a complex number is its counterpart mirrored at the real axis. That means it has the sign of the imaginary part switched.
The conjugate complex number of a + ib is a – ib.
Conjugate complex numbers become interesting if it comes to complex roots of polynomials with real components. Polynomials with real components only have pairs of conjugate complex roots (See Complex roots of a polynomials). More to this later on

As complex numbers are not just simple numbers, the calculations with them are a bit more complicate.
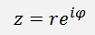
The addition and subtraction of two complex numbers is quite simple. Just the two real parts are added or subtracted and the two imaginary parts are added. The addition and subtraction should be done in the Cartesian form and that’s:
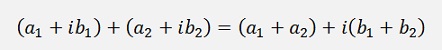

The multiplication of two complex numbers is a bit more complicate. In the Cartesian form the multiplication of two complex numbers is:

The multiplication can be carried out in polar form as well:

For the length it’s the multiplication of the length of both numbers. For the angle it’s the sum of both angles.
To proof I use the Cartesian form:
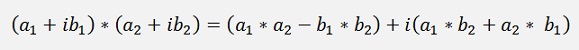
The length of this is:
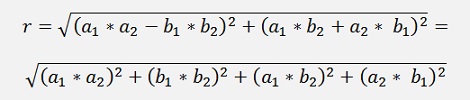
and the angle
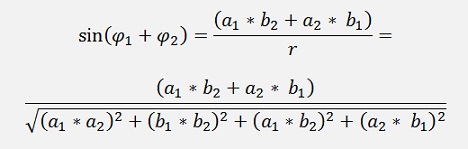
and as
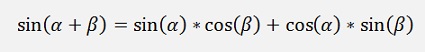
and

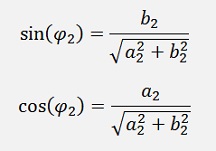
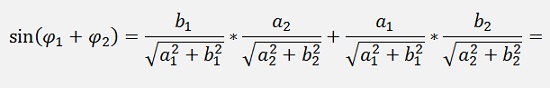
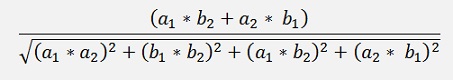
And that’s the angle of the resulting complex number.
The fact that we just have to add the angles of the two multipliers to get the resulting angle can be quite interesting if we have a polynomial with complex components and use the Horner evaluation for that. That makes for instance a first order Görtzel algorithm quite a bit easier to be understood (See first order Goertzel algorithm)
The division of two complex numbers is one more time a bit more complicate. If we just divide these numbers, we get a fraction with complex denominator
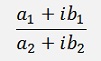
For the result we have to get rid of this complex denominator and this we can do by multiplying the denominator and the numerator by the conjugate complex number of the denominator like:
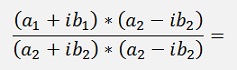

To see the relation to the polar form I check the length of this:

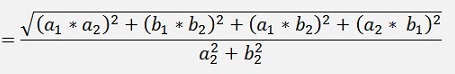
This can be written as:
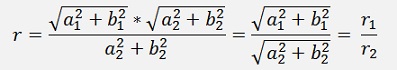
That means in the polar form we just have to divide the length of the numerator by the length of the denominator to get the resulting length of the division. For the angle we have to subtract the angle of the denominator from the angle of the numerator (as we have a multiplication by the conjugate complex number of the denominator).
To compute the root of a complex number it is the easiest to use the polar form and recall the multiplication of complex numbers in polar form and have a look at a sample:

We can say

And we know that the length of z must be the length of x to the power of 3 and the angle must be the angle of x multiplied by 3. The only problem that we have is the periodicity of the sinus and cosine. That means if z has an angle of 60°, x could have an angle of 20° which is 60° / 3. X can as well have 140° which is (60° + 360°) / 3. Or it can have 260° which is (60° + 720°) / 3. So we have 3 solutions for the angle.
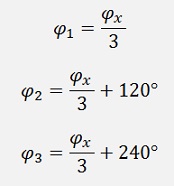
For a random root
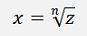
That means:
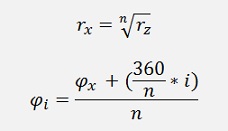
with I = 0 to n-1

