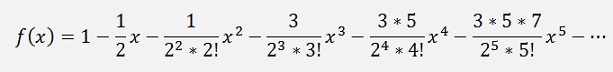Taylor polynomials
The Taylor-expansion is used to approximate a complex function by a simple polynomial. Almost every fundamental function can be approximated by a Taylor polynomial like.
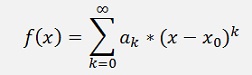
For the derivation of a Taylor polynomial we start with a polynomial like
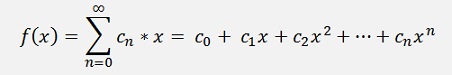
The differentiation of this is
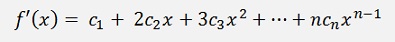
and
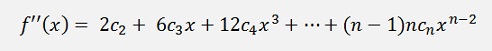
And so on
If x = 0
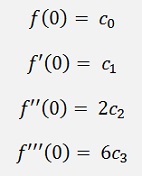
And with this
If x = 0
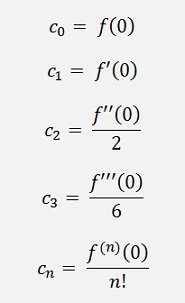
And these equations put in the polynomial
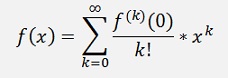
(Please note: 0! = 1)
For f(x) and computed at the position 0. But that’s not all

For a computation at a random point we have to go some steps further and substitute.
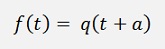
f and q are both polynomial functions and so
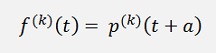
and
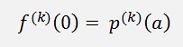
and therefore
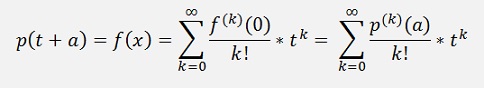
And now: If t = x - a
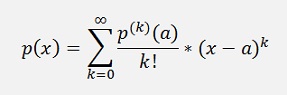
And that’s the formulation for the Taylor polynomial built at a random position “a”.
That’s quite o.k. but in the real world nobody calculates a polynomial with an infinite number of elements and if the number of elements is smaller than infinite, there is an inaccuracy.
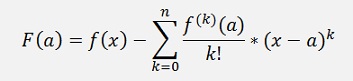
To derive the formulation for F(a) we start with two substitutions:
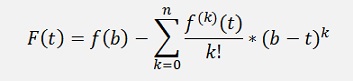
And we need the differentiation of this. According to the product rule of the differentiation (See Differential calculus)
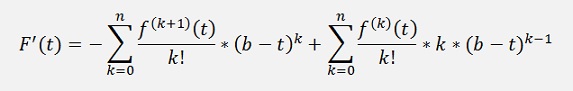
If we extract the last element of the first sum and consider that the first element of the second sum is 0, this can as well be written as:
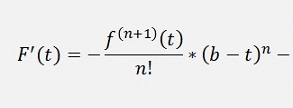
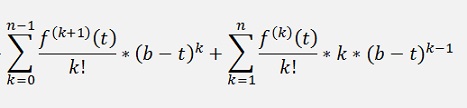
and the second sum shall start at k = 0 again:
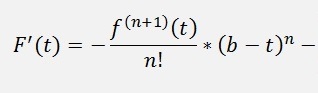
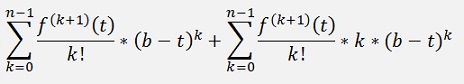
And with this:
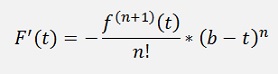
Now there comes an interesting step:
We introduce a new function
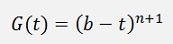
And say (according to the mean value theorem for differential calculus)
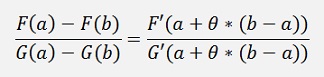
With 0 <= θ <=1
And now with
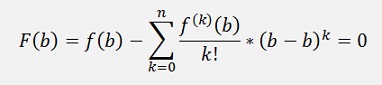
As only the first element of the sum is not 0 and this is f(b).
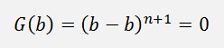
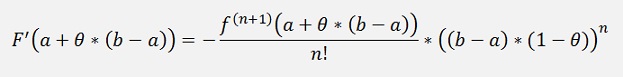
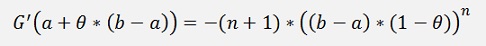
All put into the above formula:
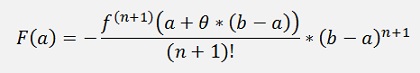
Now we can replace b by x again and get:
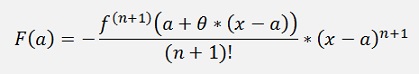
Which is Taylor’s theorem for the remainder of a Taylor polynomial of the order n. This remainder is not fully defined as θ is a random value between 0 and 1.
But never the less it’s quite well visible that it approaches 0 quite soon if n rises. The (n+1)! In the denominator becomes very big quite soon and therefore the whole expression becomes very small. That means the Taylor polynomial is a good approximation already with a relatively small order “n”.
To develop the Taylor polynomial for the sinus function is a good task to see the impact of the Taylor remainder

So we develop the Taylor polynomial for the sinus function at the position 0
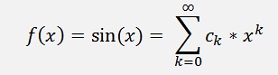
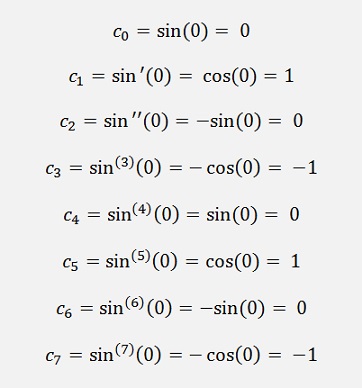
These put into the Taylor polynomial:
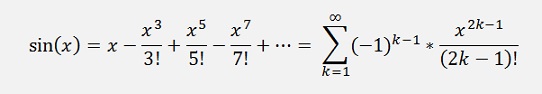
In the following graph I printed the Taylor polynomial for the sinus function with n = 1 till n = 9
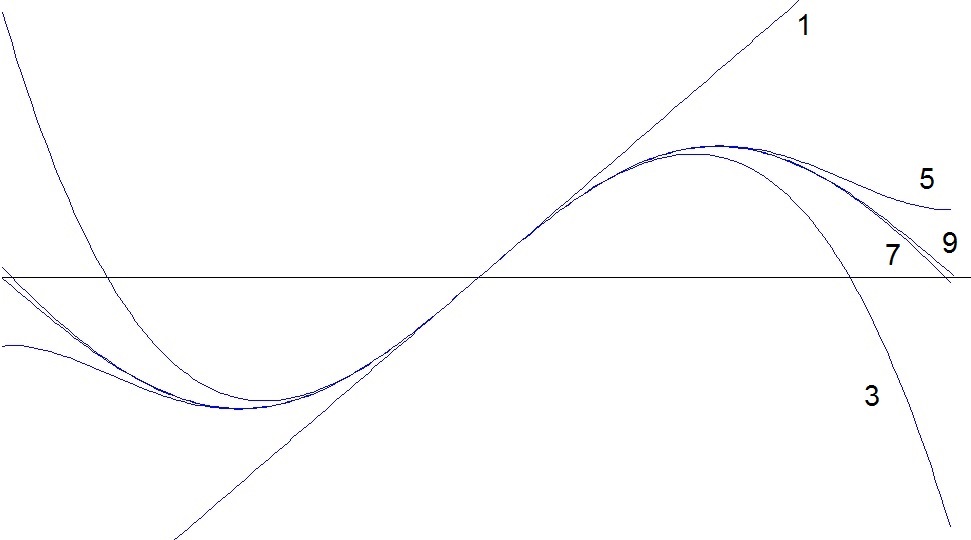
O.k. with n = 0 it’s just a straight line. That’s not too interesting. But it’s nice to see how much the shape approaches the real shape of the sinus better with each step of increasing n

In the same manner we get for Cos(x)
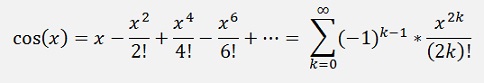
When I was working on Newton’s algorithm to compute Pi I converted the function
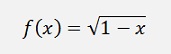
To a Taylor polynomial. That helped a lot to get to a useful formulation and therefore I document it here

First the derivations:
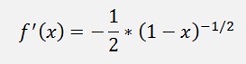
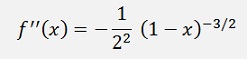
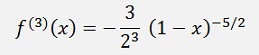
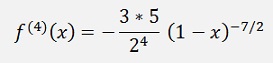

And so on.
With these we get the derivations at 0:
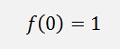

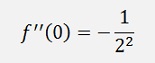
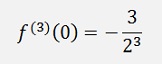
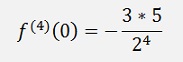
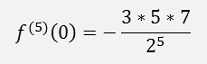
And so on.
And from them the complete polynomial: