Mosi's Math

Bessel low pass filter

The Bessel was invented by the German mathematician Friedrich Bessel (1784–1846) it is a filter type that offers an optimized transfer function for a rectangular signal. It shows a maximally flat group/phase delay (see Bessel filter on Wikipedia) . This is achieved by the transfer function

With a so called Bessel polynomial in the denominator with

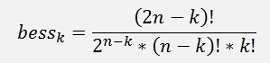
and

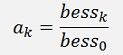
The enumerator and a0 are always 1.

With this the transfer function in s for a low pass Bessel filter for the order 1 to 4 looks like:

That can be done in small function:

public void CalcBesselPolynom(int n)
{
     int i;

     a_s = new double[n+1];
     for(i = 0; i <= n; i++)
     {
         a_s[n - i] = Fact(2 * n - i) / Math.Pow(2.0, n - i) / Fact(n - i) / Fact(i);
     }
     for (i = 0; i <= n ; i++)
     {
         a_s[i] = a_s[i] / a_s[n];
     }
}

This function calculates the Bessel polynomial backward. I switch the direction of the polynomials the way that the first element has the highest power for s. It is a bit easier to implement the polynomial multiplication like this.

So my transfer function looks like:

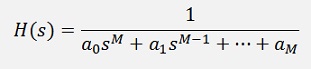
This transfer function must be converted into the transfer function in the z domain which is done by the bilinear transformation (see Digital filter design )

with

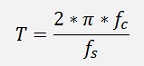
And f_c = cut off frequency of the filter and f_s = sampling frequency. This could be done manually of course. But an algorithm can do that automatically :-)

Therefore I rewrote the transfer function to

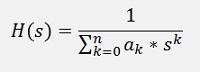
And with the bilinear transformation:

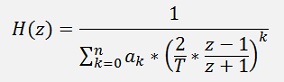
In this equation we have to get rid of the fraction in the denominator. Therefore each element of the sum must be extended by (z + 1)^n-k and the enumerator becomes (z + 1)ⁿ.

Now in the Bessel filter there comes a magic correction factor :-)

The -3 dB frequency is shifted to some higher value when the order of the filter gets higher in the Bessel filter. Therefore there is a correction to be done like:

and

The transformation into the z domain I implemented with a list of double arrays to have the possibility to grow the arrays dynamically:

public List<double[]> aa = new List<double[]>();

The only disadvantage of this approach is that I cannot modify one single element of this list. So I have to remove the element from the list and replace it by the modified one. That looks like:

double[] tempA = new double[2];
tempA[0] = 1.0;
tempA[1] = 1.0;
for (i = 0; i <= order; i++)
{
     double[] tempEl = aa.ElementAt(i);
     tempEl = Poly.Mult(Poly.Power(tempA, i), Poly.Power(tempEl, order - i));
     tempEl = Poly.Mult(tempEl, a_s[i] * Math.Pow(2.0 / tc, order - i));
     aa.RemoveAt(i);
     aa.Insert(i, tempEl);
}

That gives a polynomial in z for each a_k. These polynomials must be added together to one polynomial containing the elements a_i for each z^k of the transfer function.

That’s done with:

for (i = 0; i <= order; i++)
{
     a_z[i] = 0;
     for (j = 0; j <= aa.Count-1; j++)
     a_z[i] = a_z[i] + aa.ElementAt(j)[i];
}

Now the array a_z contains the elements a_i.

The elements bi must be computed as well

tempA[0] = 1.0;
tempA[1] = 1.0;
b_z = Poly.Power(tempA, order);

and finally we need to have a₀ = 1 and therefore each element must be divided by a₀.

for (i =0; i < b_z.Length; i++)
{
b_z [i] = b_z [i] / a_z[0];
}
for (i = order; i >= 0; i--)
{
a_z[i] = a_z [i] / a_z [0];
}

After this a_z and b_z contain the filter parameters.

In the literature this function usually looks like:

As M = N here that’s no difference for the implementation. Just divide the enumerator and denominator by z^N. The a and b parameters remain the same and they can be used as they are.

The formulation for the filter sequence is

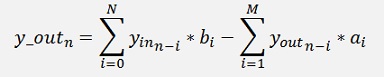
(and here M = N)This formulation says that the last M-1 elements of the output data are used. These values are not available in the beginning. Therefore the first N elements of the output must be treated different like:

for (i = 0; i < order; i++)
{
     y_out[i] = 0;
     for (j = 0; j <= i; j++)
     {
         y_out[i] = y_out[i] + y_in[i-j] * zb[j];
     }
     for (j = 1; j <= i; j++)
     {
         y_out[i] = y_out[i] - y_out[i-j] * za[j];
     }
}

And the rest

for (i = order; i < datapoints; i++)
{
     y_out[i] = 0;
     for (j = 0; j <= order; j++)
     {
         y_out[i] = y_out[i] + y_in[i - j] * zb[j];
     }
     for (j = 1; j <= order; j++)
     {
         y_out[i] = y_out[i] - y_out[i - j] * za[j];
     }
}

A Bessel filter of 2. , 4. or 6. order with the cut off frequency of 300 Hz produces this transfer function:

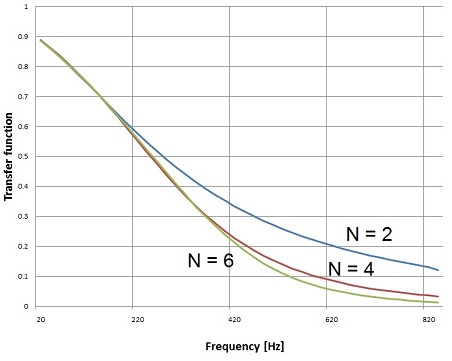
The jump from 4. to 6. order seems not to be too big in the steepest area both orders are almost equal and the filter principally has a rather flat transfer function but if we look at a (red) signal of 20 Hz with a noise frequency of 1000 Hz like

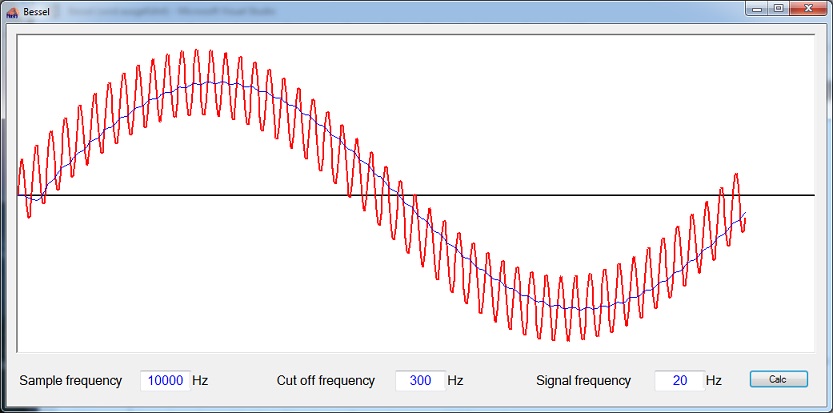
The Bessel filter of 4. order and cut off frequency 300 Hz almost removes this noise fully (blue curve). That looks quite cool :-)

C# Demo Project Besssel filter

Bessel.zip