The Butterworth low pass filter is a filter type with a constant transfer function in the passband and stopband. It’s transfer function decreases monotone for an increasing f and its slope is -20*N dB/decade. For f = 0 the transfer function returns 1
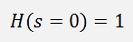
The general transfer function of the low pass Butterworth filter looks like:
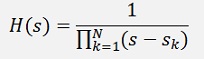
The poles of this transfer function are complex:
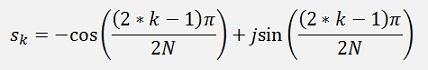
In the literature there is often a form like
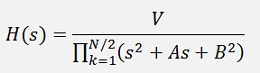
used for the transfer function. That comes from the fact that the poles are always conjugate complex. The poles are lying on the left side of a circle like

And we always have conjugate complex pairs. Her for instance for N = 4
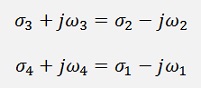
these pairs are multiplied together like
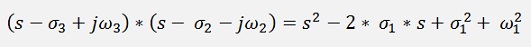
and her we have

and so
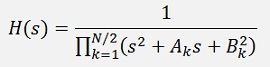
with
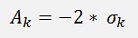

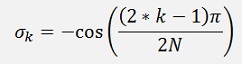
If N is odd we get a little different situation

One pole is pure real here and we get

with

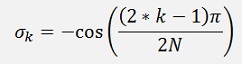
With this the transfer function in s for a low pass Bessel filter for the order 1 to 4 looks like:

These parameters are independent on fs and fc. They depend only on the order of the filter.
Implemented in a C# function that would be:
public void CalcButterworth(int order)
{
int i = 1;
double[] poly = new double[3];
double[] poly2 = new double[2];
poly[0] = 1.0;
if (order % 2 == 0)
{
poly[2] = 1.0;
for (i = 1; i <= order / 2; i++)
{
poly[1] = 2.0 * Math.Cos((2 * i - 1) * Math.PI / 2 / order);
a_s = Poly.Mult(a_s, poly);
}
}
else
{
poly2[0] = 1.0;
poly2[1] = 1.0;
a_s = Poly.Mult(a_s, poly2);
poly[2] = 1.0;
for (i = 2; i <= (order + 1) / 2; i++)
{
poly[1] = 2.0 * Math.Cos((i - 1) * Math.PI / order);
a_s = Poly.Mult(a_s, poly);
}
}
}
This function calculates the denominator of the transfer function in the Laplace domain and puts it the array a_s. This transfer function must be transformed into the z domain. There the frequencies get into the game.The transformation is done, the same way I did it in Digital filter design, by a bilinear transformation with

and
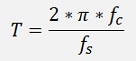
with fc = cut off frequency of the filter and fs = sampling frequency.
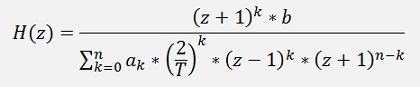
The function for this transformation is more or less the same as I used it in the Bessel filter.
public void TransformToZPlane()
{
int i, j;
double[] tempA = new double[2];
List<double[]> aa = new List<double[]>();
for (i = 0; i <= order; i++)
{
aa.Add(new double[] { 1, -1 });
}
tempA[0] = 1;
tempA[1] = 1;
b_z = Poly.Power(tempA, order);
for (i = 0; i <= order; i++)
{
double[] tempEl = aa.ElementAt(i);
tempEl = Poly.Mult(Poly.Power(tempA, i), Poly.Power(tempEl, order - i));
tempEl = Poly.Mult(tempEl, a_s[i] * Math.Pow(2.0 / tc, order - i));
aa.RemoveAt(i);
aa.Insert(i, tempEl);
}
for (i = 0; i <= order; i++)
{
a_z[i] = 0;
for (j = 0; j <= order; j++)
a_z[i] = a_z[i] + aa.ElementAt(j)[i];
}
for (i =0; i < b_z.Length; i++)
{
b_z[i] = b_z[i] / a_z[0];
}
for (i = order; i >= 0; i--)
{
a_z[i] = a_z[i] / a_z[0];
}
}
This function computes the transfer function in the z plane and puts it into the arrays a_z and b_z. I initialize the parameters like
public int order = 4;
double fs = 10000.0;
double fc = 300.0;
and with these I get the transfer function
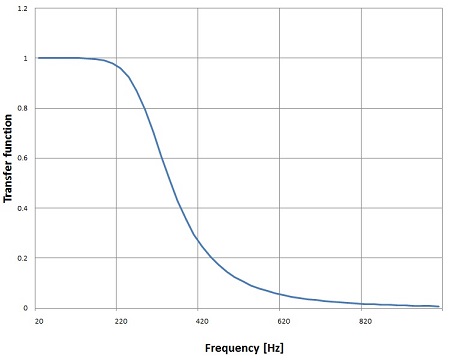
With quite a steep slope

High pass filter
The transformation of the low pass filter into a high pass filter is done by a so called low-pass to high-pass transformation. That just means to replace s by 1/s in the Laplace domain. In the transfer function like
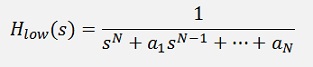
That is

or without compound fraction
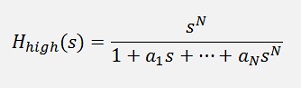
In the implementation that means I would have to switch the direction of the elements of my denominator polynomial. But as the Butterworth always has symmetric elements in the denominator I can leave that and need just to add the SN in the enumerator. This can be done in the transformation from Laplace to z domain. The following modification in the function TransformToZPlane() does this
public void TransformToZPlane(bool bHighPass)
{
int i, j;
double[] tempA = new double[2];
tempA[0] = 1;
if (bHighPass)
{
tempA[1] = -1;
b_z = Poly.Power(tempA, order);
b_z = Poly.Mult(b_z, Math.Pow(2.0 / tc, order));
}
else
{
tempA[1] = 1;
b_z = Poly.Power(tempA, order);
}
tempA[1] = 1;
With this small modification the filter can work as high pass filter as well and shows a transfer function of

The demo project consists of one main window. It processes a short sample signal (red curve) and displays the filtered signal (blue curve) the cut off frequency, sampling frequency and signal frequency can be set and in the left upper corner of the graphic is a checkbox where high or low pass behaviour can be selected.

A online solver in JavaScript, that returns the filter parameters, can be found on Butterworth filter
C# Demo Project Butterworth filter

