Discrete Fourier transformation
Basic DFT algorithm with complex numbers
According to the main clause of Fourier a signal f(n) that is periodic within N and we have N samples of it can be transformed into its Fourier components as follows:

DFT

with

DFT

DFT


Another equation for the complex Fourier components ck looks like

DFT

DFT


That means the complex Fourier component ck is a complex sum of complex products of f(n) and complex vectors spinning around the unit circle. For a complete Fourier transformation we would need N Fourier components (ck) and for each component we need N sine and N cosine values. For 1000 samples that would be 1 million sine and cosine values to be calculated. That consumes a lot of CPU power and time. But it works


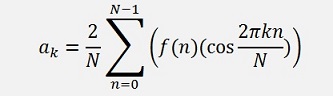
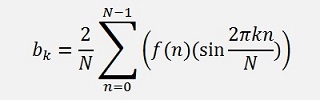
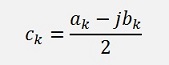
and in C# it looks like:


public void CalcDFT(int N)
{
int k, n;
TKomplex w;
if (N > 0)
{
for (k = 0; k < N; k++)
{
c[k].real = 0;
c[k].imag = 0;
for (n = 0; n < N; n++)
{
w.real = Math.Cos((double)(2.0 * Math.PI * (double)(k * n) / (double)(N)));
w.imag = -Math.Sin((double)(2.0 * Math.PI * (double)(k * n) / (double)(N)));
c[k] = ksum(c[k], kprod(w, y[n]));
}
c[k].real = c[k].real / (double)(N) * 2.0;
c[k].imag = -c[k].imag / (double)(N) * 2.0;
}
}
c[0].real = c[0].real / 2;
c[0].imag = c[0].imag / 2;
}



Calculated by this standard implementation a Fourier transformation of 1000 samples took 140 ms on my computer (there are certainly faster computers on this world :-) )

The source of this standard implementation can be found in the Visual C# project DFT_std.

The functions ksum() and kprod() are simple functions for complex addition and multiplication


public TKomplex ksum(TKomplex a, TKomplex b)
{
TKomplex res;
res.real = a.real + b.real;
res.imag = a.imag + b.imag;
return (res);
}

 

public TKomplex kprod(TKomplex a, TKomplex b)
{
TKomplex res;
res.real = a.real * b.real - a.imag * b.imag;
res.imag = a.real * b.imag + a.imag * b.real;
return (res);
}



Considerations about periodicity
Now, the sine and the cosine function both are periodic to 2π and for k = 1 we have to calculate both, sine and cosine for the values 0 to 2π with step size 2π /N. For k = 2 we have 0 to 4 π with step size 2/N and so on. So we get for k = 2 the same values as we got them already for k = 1. Only, we get each second one and when n gets bigger than N/2 we finished one round of the unit circle and start again at the same values as for n = 0. The bigger k becomes the bigger the steps become and the more rounds of the unit circle we pass. But the sine and the cosine values we get are still the same as we got them for k = 1. That means it’s basically enough just to calculate N sine and N cosine value between 0 and 2π with step size 2π/N and keep them in a look up table for the entire transformation. For 1000 samples we just have to calculate 1000 sine and 1000 cosine values instead of 999000 and that saves quite some time.


We build the look up table with:

for (k = 1; k < N; k++)

{

we[k].real = Math.Cos((2.0 * Math.PI * (double)(k) / (double)(N)));

we[k].imag = -Math.Sin((2.0 * Math.PI * (double)(k) / (double)(N)));

}




And the corresponding sine and cosine values we can obtain from the look up table by a simple modulo division of k * n by N. Like this the discrete Fourier transformation becomes not “fast” but quite “quick” and lean :-)


public void CalcDFT()   //  Quick and lean Fourier transformation
{
int k, n;
if (N > 0)
{
for (k = 0; k < N; k++)
{
c[k].real = 0;
c[k].imag = 0;
for (n = 0; n < (N - 1); n++)
{
c[k] = ksum(c[k], kprod(we[(k * n) % N], y[n]));
}
c[k].real = c[k].real / N * 2;
c[k].imag = -c[k].imag / N * 2;
}
c[0].real = c[0].real / 2;
c[0].imag = c[0].imag / 2;
}
}



This implementation takes 53 ms for the same 1000 samples as the above mentioned. Quite a bit quicker.

The code to this implementation is in DFT_lean.



Complex numbers?
Now there came some more considerations into my mind. In the main clause there are no complex numbers. The input is a sequence of real numbers (at least in my application coming from electric signal analysis ) and we end up with another sequence of real numbers. So, why do we use complex numbers in the middle?

We have a complex multiplication and a complex addition in our algorithm. So let’s have a look at them. First the multiplication we[x] * y[n]. That looks like

(we[x].re * y[n].re - we[x].im * y[n].im) + j(we[x].re * y[n].im + we[x].im * y[n].re)

y[n].im is always 0 and therefore the second and the third part are also 0 and our complex multiplication reduces to

(we[x].re * y[n].re) + j(we[x].im * y[n].re)


And that means

y[n].re * cosine(x) + j(y[n].re * sine(x))

That looks quite like ak and bk of the main clause. In the following addition we just have to sum the real parts and the imaginary parts. So there is no mixing of imaginary and real part in the complete calculation and finally we get the ak part in the real part of ck and the bk part in the imaginary part of ck and we can forget about all the complex stuff :-)

With the limitation that the input sequence does not contain imaginary numbers we can implement the Fourier transformation without complex numbers:


public void CalcDFT()
{
int k, n;
if (N > 0)
{
for (k = 0; k < N; k++)
{
a[k] = 0;
b[k] = 0;
for (n = 0; n < (N - 1); n++)
{
a[k] = a[k] + ((cosine[(k * n) % N] * y[n]));
b[k] = b[k] + ((sine[(k * n) % N] * y[n]));
}
a[k] = a[k] / N * 2;
b[k] = b[k] / N * 2;
}
a[0] = a[0] / 2;
b[0] = b[0] / 2;
}
}



The initialisation becomes like this

public TFftAlgorithm(int order)
{
int k;
N = order;
y = new double[N + 1];
a = new double[N + 1];
b = new double[N + 1];
xw = new double[N + 1];
sine = new double[N + 1];
cosine = new double[N + 1];
 
cosine[0] = 1.0;    // we don't have to calculate cos(0) = 1
sine[0]   = 0;      //                        and sin(0) = 0
for (k = 1; k < N; k++) //  init vectors of unit circle
{
cosine[k] = Math.Cos((2.0 * Math.PI * (double)(k) / (double)(N)));
sine[k] = Math.Sin((2.0 * Math.PI * (double)(k) / (double)(N)));
}
}



Whit this implementation the 1000 samples were transformed in 20 ms. That’s almost 5 times quicker than the first implementation at the top of this article. It’s not an fast Fourier transformation. But it’s at least it’s a quick Fourier transformation and it looks quite lean.

This implementation is in the project DFT_lean_quick.

Whit the rectangle signal the result should look like this:

DFT



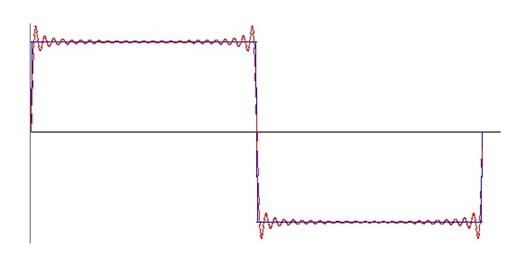
For the analytic Fourier transformation of the used sample signals see Fourier transformation.

And keep in mind that only the first N/2 harmonics can be used. The harmonics N/2+1 to N-1 are mirrored from the harmonics 0 to N/2.




C# Demo Projects to Fourier transformation
  • DFT_std.zip

  • DFT_lean.zip

  • DFT_lean_quick.zip




    • Java Demo Project to Fourier transformation
  • DFT_lean_quick.zip