For the transformation Jacobi first multiplies the transposed matrix UT by A and second the resulting matrix A’ by U and gets A’’:
Such a transformation should eliminate two elements of the matrix A symmetric to the main diagonal. I write “should” because it does not really. It just brings the elements close to 0. But if the same transformation is done several times it will do so.
So the sequence is to start at a21 and a12, determine the transformation matrix and bring these two elements closer to 0. Then go on to a31 and a13 and bring them closer to 0. Do this for all elements except the ones of the main diagonal. Then starting at a21 and a12 again and bring these elements even closer to 0 in a second loop and so on until all the elements are close enough to 0.
The basic rotation matrix U(p, q, φ) used for these transformations looks like:
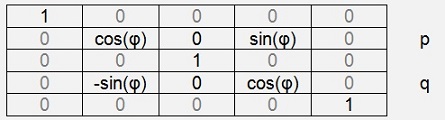
and we have to compute the angle φ to eliminate the element apq with the transformation by this matrix.
Multiplying UT by A gives for the affected elements:
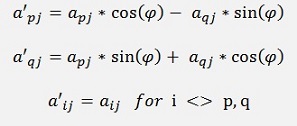
for j = 1,2,…n
and multiplying the resulting A’ by U
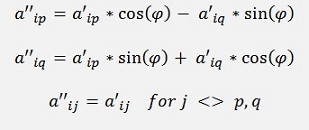
for i = 1,2,…n
These equations resolved for a’’pq is:
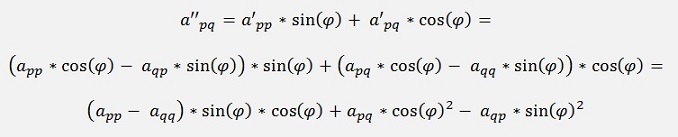
and as the matrix A is symmetric apq = aqp and we get:
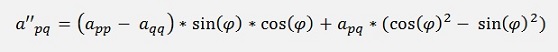
Now the element a’’pq shall become 0. That means:
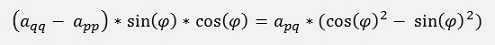
and therefore
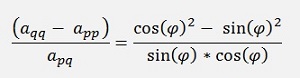
both sides of this equation are divided by 2 for later on and we substitute
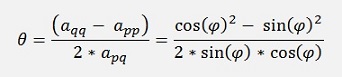
We have θ as a function of app, aqq and apq. And on the other side we have cos(φ) and sin(φ) which we are looking for.
If we use
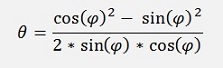
and extend the denominator and enumerator by 1/ cos(φ)2, we get:
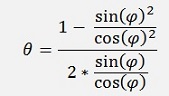
and with t = tan(φ) = sin(φ)/ cos(φ)
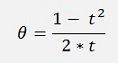
This converted a bit
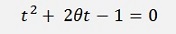
and extended by + θ2 – θ2:

and this can be written as
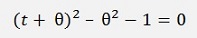
or
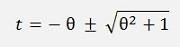
or as well as
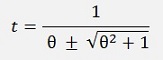
From these two results we use to smaller one and say
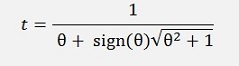
for θ <> 0
and
for θ = 0
and finally for the angle we are looking for:
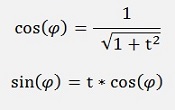
With this we have the elements of the rotation matrix U.
I put this into a function CalcRMatrix() as follows:
public void CalcRMatrix(double[,] a, int p, int q, int size)
{
int i, j;
double phi;
double t;
phi = (a[q, q] - a[p, p]) / 2 / a[q, p];
if (phi != 0)
{
if (phi > 0)
t = 1/(phi + Math.Sqrt(phi * phi + 1.0));
else
t = 1/(phi - Math.Sqrt(phi * phi + 1.0));
}
else
t = 1.0;
for (i = 0; i < size; i++)
{
for (j = 0; j < size; j++)
{
r[i, j] = 0.0;
}
r[i, i] = 1.0;
}
r[p, p] = 1 / Math.Sqrt(t * t + 1.0);
r[p, q] = t * r[p, p];
r[q, q] = r[p, p];
r[q, p] = -r[p, q];
}
This function calculates the sin(φ) and cos(φ) values to eliminate the element apq and writes them into the matrix R. Now we first have to multiply the transposed of this rotation matrix RT by A and the multiply the resulting A’ by R. For these multiplications there are some interesting details to consider:
The rotation matrix has the following form:
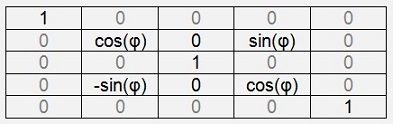
For the transposed matrix only the sign of the two sinus values switches or we can switch the indexing for x and y in the multiplication. That’s what I did in my function MultTranspMatrixLeft().
In the rotation matrix all the rows except p and q only have one element not zero: The diagonal element that means if we multiply this rotation matrix by another matrix from the left side only the rows p and q will affect the other matrix. All the elements in the other rows will remain the same.
If the rotation matrix is multiplied by another matrix from the right side, only the columns p and q will affect the other matrix.
That means we just need to handle these two rows or columns for a multiplication as:
public double[,] MultTranspMatrixLeft(double[,] a, double[,] m, int p, int q, int size)
{
int j, k;
double[,] al = new double[2, size];
for (j = 0; j < size; j++)
{
al[0, j] = 0.0;
al[1, j] = 0.0;
for (k = 0; k < size; k++)
{
al[0, j] = al[0, j] + (m[k, p] * a[k, j]);
al[1, j] = al[1, j] + (m[k, q] * a[k, j]);
}
}
for (j = 0; j < size; j++)
{
a[p, j] = al[0, j];
a[q, j] = al[1, j];
}
return a;
}
This function carries out the multiplication of the transposed matrix m from the left side by the matrix a and returns the result in a.
public double[,] MultMatrixRight(double[,] a, double[,] m, int p, int q, int size)
{
int i, j, k;
double[,] al = new double[size, 2];
for (i = 0; i < size; i++)
{
al[i, 0] = 0.0;
al[i, 1] = 0.0;
for (k = 0; k < size; k++)
{
al[i, 0] = al[i, 0] + (a[i, k] * m[k, p]);
al[i, 1] = al[i, 1] + (a[i, k] * m[k, q]);
}
}
for (i = 0; i < size; i++)
{
a[i, p] = al[i, 0];
a[i, q] = al[i, 1];
}
return a;
}
Multiplies m from the right side by matrix a and returns the result in matrix a.
With these functions one iteration can be run as
for (i = 0; i < maxOrder; i++)
{
for (k = i + 1; k < maxOrder; k++)
{
if (a[k, i] != 0.0)
{
CalcRMatrix(a, i, k, maxOrder);
a = MultTranspMatrixLeft(a, r, i, k, maxOrder);
a = MultMatrixRight(a, r, i, k, maxOrder);
}
}
}
One such iteration brings all elements except the ones in the main diagonal a bit closer to 0 and we have to repeat it until all elements are close enough to 0 that we can regard them as 0. To check whether the elements are close enough to 0 or not it’s enough just to look at the elements right below the main diagonal. If they can be considered as 0 that’s o.k. At the end of these loops we have a diagonal matrix and the elements in the main diagonal are the Eigenvalues.
For the eigenvectors we just have to multiply a unit matrix by all the rotation matrixes and at the end all the eigenvectors are the columns of the resulting matrix. I use the matrix v for this, initialise it as unit matrix and multiply it as
v = MultMatrixRight(v, r, i, k, maxOrder);
in each loop. The entire calculation I put into the function RunJacobi().
With a sample matrix of
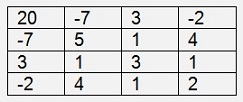
I get the Eigenvalues

And the eigenvectors to the eigenvalues in the corresponding column
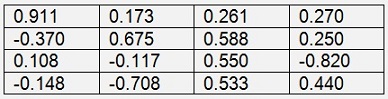
As symmetric matrixes only have real eigenvalues the eigenvectors have only real elements to.$
But remark: This is valid for symmetric matrixes only.

