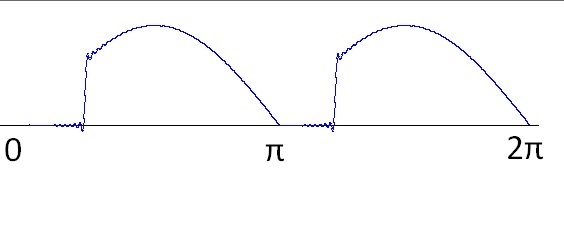
The rectified cut sinus signal is the classic output signal of a DC power supply without filtering. It’s interesting to see how much noise in form of harmonics this signal contains
Starting with the ak components:
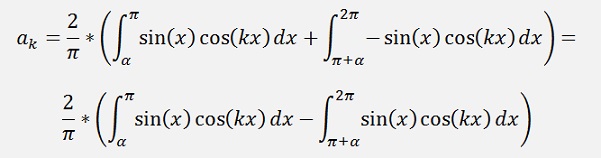
as
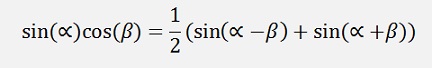
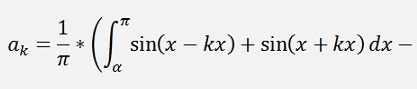
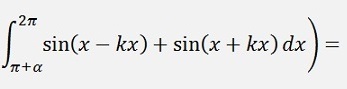
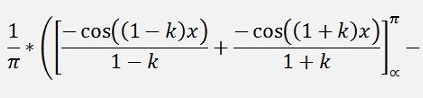
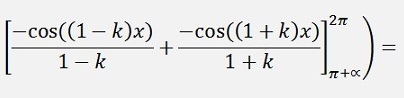
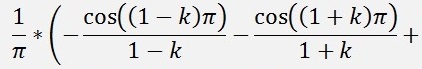
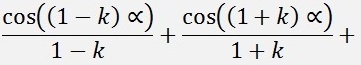
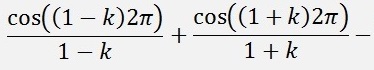
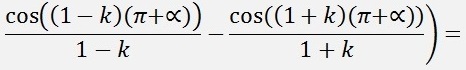
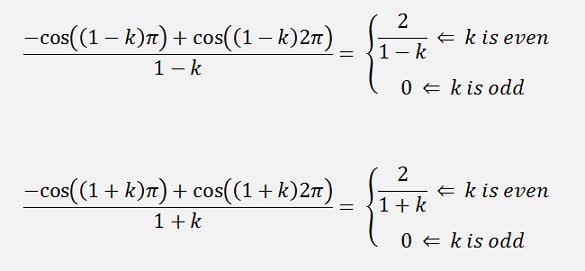
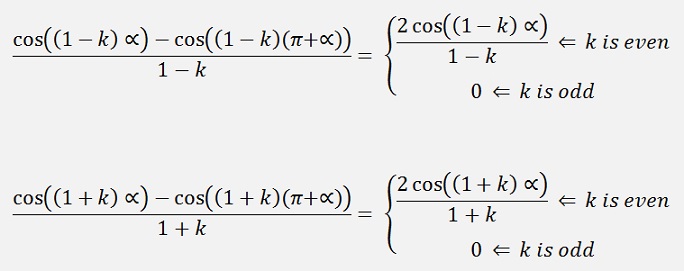
If k is even
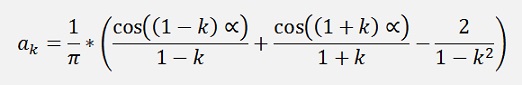
If k is odd
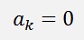
Now the bk components:
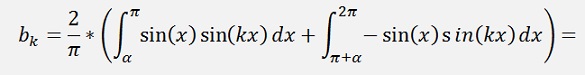
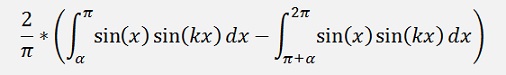
as
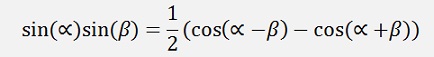
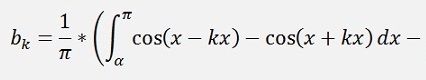
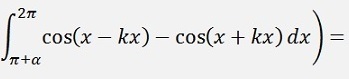
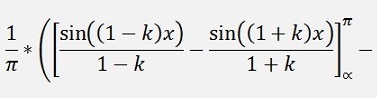
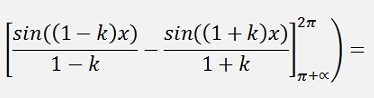
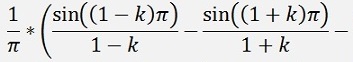
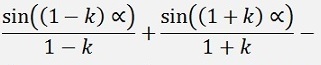
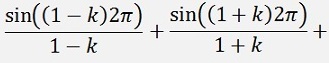
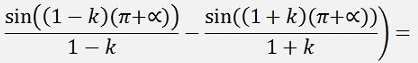
as
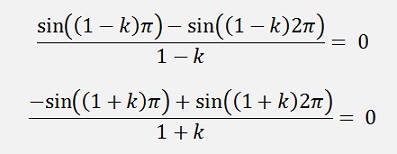
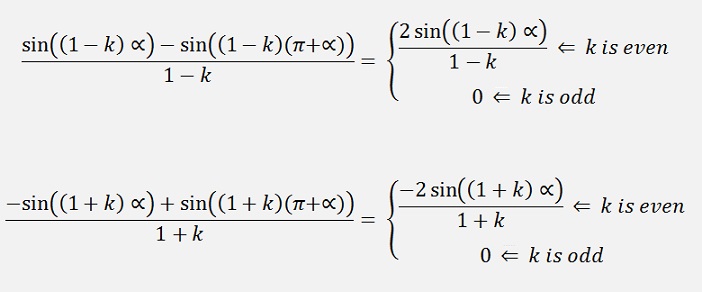
If k is even
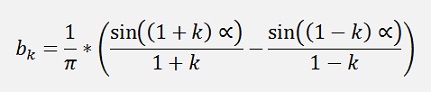
If k is 0dd
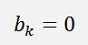
Put into code with ak as the real parts and bk as the imaginary parts:
private void SinusRectifiedCut(double peak, double alpha)
{
int
j;
c[0].real = peak / Math.PI * (1.0 + Math.Cos(alpha));
for (j = 1; j < 500; j++)
{
}c[0].real = peak / Math.PI * (1.0 + Math.Cos(alpha));
for (j = 1; j < 500; j++)
{
if
(j % 2 != 0)
{
else
{
}{
c[j].real
= 0;
c[j].imag = 0;
}c[j].imag = 0;
else
{
c[j].real
= peak / Math.PI
* (Math.Cos(alpha
* (1.0 -
j)) / (1.0 - j) + Math.Cos(alpha
* (1.0 +
j)) / (1.0 + j) + 2.0 / (1.0 - j * j));
c[j].imag = peak / Math.PI * (Math.Sin(alpha * (1.0 + j)) / (1.0 + j) - Math.Sin(alpha * (1.0 - j)) / (1.0 - j));
}c[j].imag = peak / Math.PI * (Math.Sin(alpha * (1.0 + j)) / (1.0 + j) - Math.Sin(alpha * (1.0 - j)) / (1.0 - j));
And the spectrum for α = 40° and the first 30 harmonics:
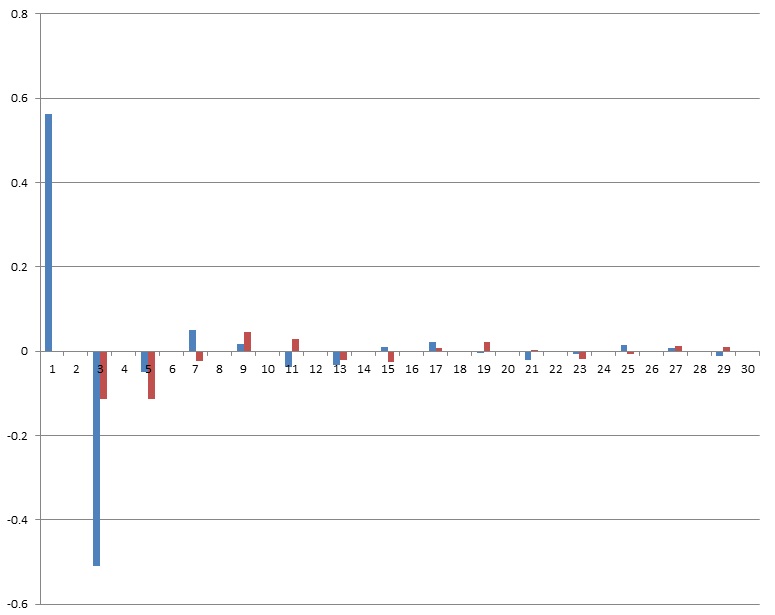
The blue bars are the real elements and red the imaginary parts.
And if all the harmonics are put together, we get the origin signal shape.
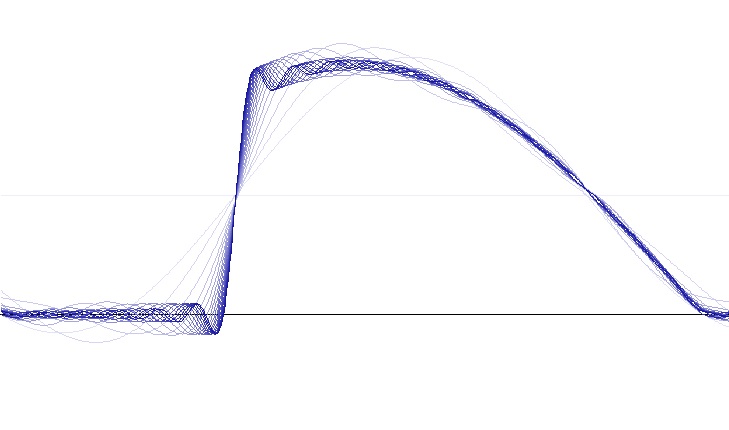
The brightest line is the base frequency. The next darker is the base frequency plus the first harmonic, then comes the same plus the next harmonic … and so on. The more harmonics are included, the closer the shape approximates the origin shape

C# Demo Project Fourier signals

