Triangle signal

To calculate the Fourier transformation of a triangle signal it’s a good approach to start with the following signal shape. That keeps the calculations easy.

Peak = π/2 :-)


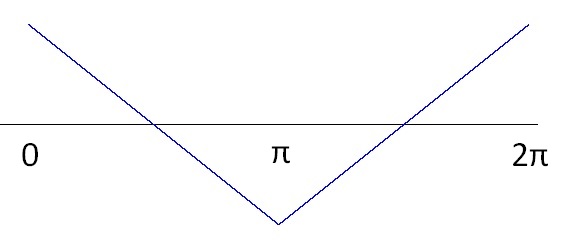
Triangle

Triangle


For the ak components:


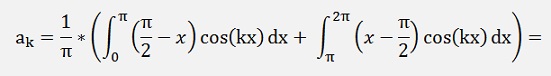
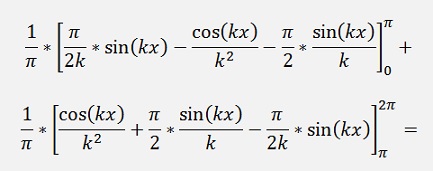
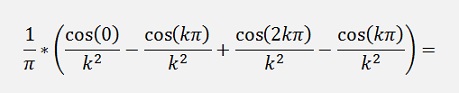
Triangle

Triangle

Triangle


If k is odd


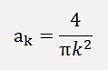
Triangle


If k is even


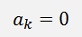
Triangle


For the bk components:


As the function is even:


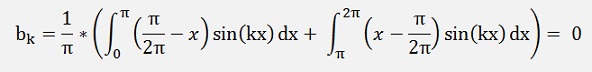
Triangle


Now if peak = h instead of π/2

If  k is odd



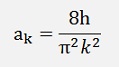
Triangle


If k is even



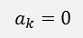
Triangle


Now we shift the signal as much to the right to get the final shape (that’s –π/2):



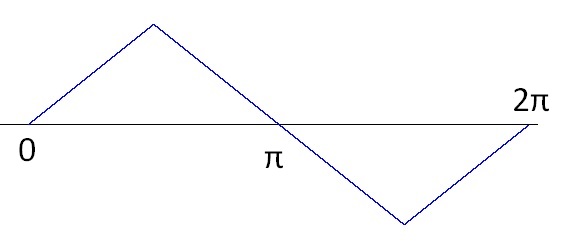
Triangle


As this wave form is –π/2 phase shifted and with the following considerations:



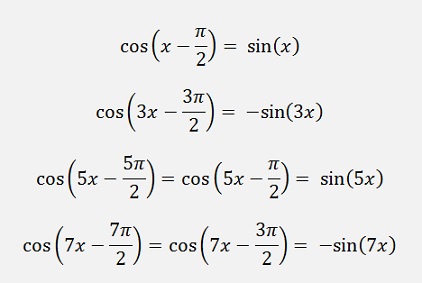
Triangle


…

we get

If k is odd



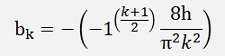
Triangle


If k is even


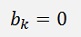
Triangle


and


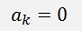
Triangle


Implemented into a function that is:



private void Triangle(double peak)
{
int j;
double sign = 1.0;
for (j = 1; j < 500; j++)
{
c[j].real = 0;
if (j % 2 == 0)
c[j].imag = 0;
else
{
c[j].imag = sign * peak * 8 / Math.PI / Math.PI / j / j;
sign = -sign;
}
}
}




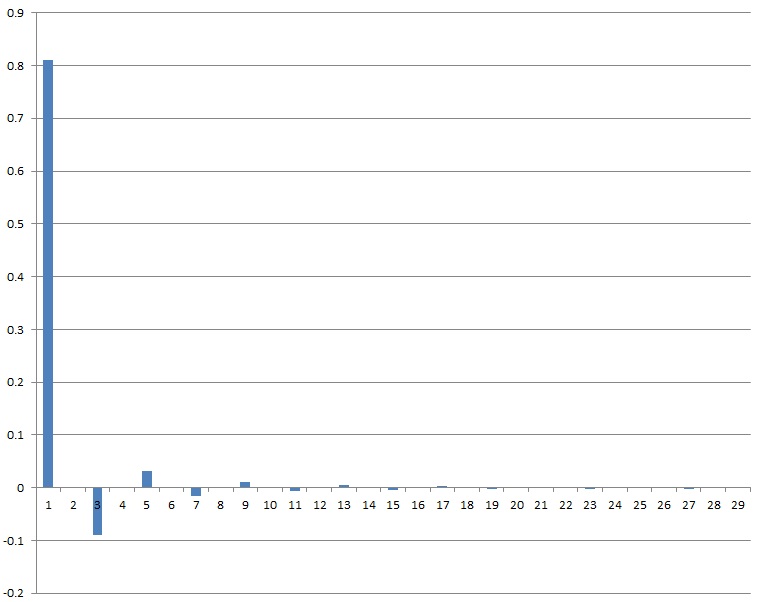
And that creates the following spectrum for the first 30 harmonics:

Triangle


C# Demo Project Fourier signals
  • FourierSignals.zip


    • Java Demo Project Fourier signals
  • FourierSignals.zip