The Romberg integration is basically an approximated integration by a combination of the Trapezoidal Rule and the Richardson extrapolation to solve an definite integral of a continuous function f(x).

The basic Trapezoidal Rule builds a sequence of Trapezoidal squares below the shape of the function to be integrated and computes the area of these squares.

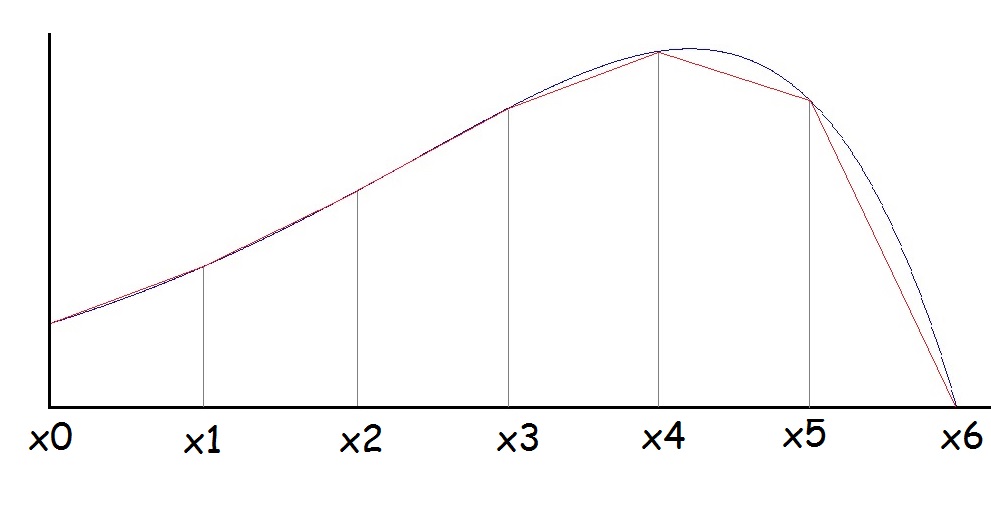
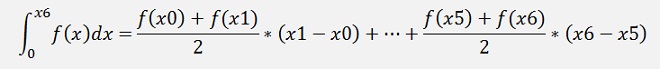
And with

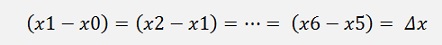
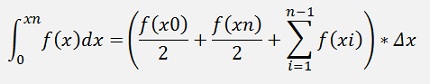
Here with n = 6


If we have a starting point a and an endpoint b:

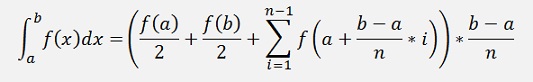
Here with n = 6



In a simple function that’s like:

private double Calcrapezodial(int n)
{
     int i;
     h = (b - a) / n;
     m = (f_x(a) + f_x(b)) / 2;
     for (i = 1; i < n; i++)
     {
         m = m + f_x(a + h * i);
     }
     m = m * h;
     return m;
}



With f_x() as the function to be integrated and h as the delta(x), the width of one trapezoid.

Werner Romberg used the following estimation for the cut off error of the trapezoidal method:

If T(h) is the approximated integral of f(x) from a to b and I is the accurate integral of it, the cut off error is

(Shall nobody ask where that comes from. Its derivation would be a hell of complicate I heard. I just believe it as it is ) It’s related to h2. That led Romberg to the idea that this cut off error can be expressed as a polynomial of h² like:

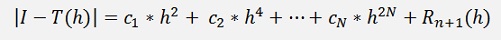
With c_i as constants independent on h and h as the width of one trapezoid again.

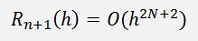
A small residue at the end.


To this idea Romberg applied the Richardson extrapolation:


If we set up the formulation for the cut off error for h/2. That is

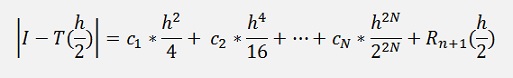
A small residue at the end.
Multiply that by 4 and subtract the above formulation from it

the part c₁ * h² drops out.



Now Romberg says, if the function to be integrated is rather smooth, c₁ > c₂ > c₃ >….> c_N and therefore this subtraction reduces the cut off error.

Now recall: T(h) is the approximated integral for the given trapezoid width h and T(h/2) is the approximation for half the width. If we subtract T(h) – 4T(h/2), we get a new approximation that is 3 times as big but has a smaller cut off error. If we divide this by 3 we get a much better approximation than T(h) and T(h/2) are. This is the basic Richardson extrapolation. But this is not all.

Romberg went a bit further and said: Why not doing this same procedure for h/4, h/8, h/16 and say

and

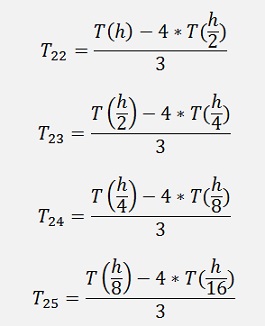
And with these approximations we do the same again but as in these approximations the h² part in the cut off error has already vanished we can remove the h⁴ part by subtracting the second approximation multiplied by 16 and dividing by 15:

That leads to 3 new approximations that are even more accurate than the 4 above ones.

And with these we do the same again to remove the h⁸ term of the cut off error by:

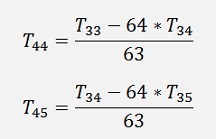
and from these finally

We get the h¹⁶ part of the cut off error removed and a very accurate approximation for our integral for a minimum width of the trapezoids of (b-a)/16. For the sample from above that looks like:

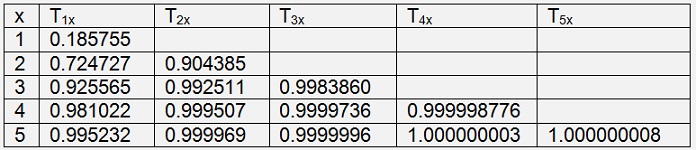
T₁₅ = 0.995232 and has an error of 0.0048 whereas T₅₅ = 1.000000008 and has an error of 0.000000002 only by applying the Richardson extrapolation a few times. That’s quite cool




Now, to put that all into an algorithm, we first have to compute the T_1x values and from these the Richardson extrapolations in the triangle as shown above with.

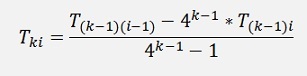
If the loop for i is started at N, for T a 1 dimensional array can be used.


This put in a small procedure is:

private double CalcRomberg(int N)
{
     int i, j, k;
     double d;
     h = b - a;
     //trapezoidal rule
     for (j = 1; j <= J; j++)
     {
         m[j - 1] = f_x(a) + f_x(b);
         k = (int)Math.Pow(2, j - 1);
         for (i = 1; i < k; i++)
         {
              d = f_x(a + h * i);
              m[j - 1] = m[j - 1] + 2 * d;
         }
         m[j - 1] = m[j - 1] * h / 2;
         h = h / 2;
     }
     // Richardson extrapolation
     for (k = 1; k < J; k++)
     {
         for (i = J - 1; i >= k; i--)
         {
              m[i] = (Math.Pow(4, k) * m[i] - m[i - 1]) / (Math.Pow(4, k) - 1);
         }
         m[i] = 0; // just for a better visualisation :-)
     }
     return t[N - 1];
}

IntegrationTrapezodial.zip

IntegrationRomberg.zip