Thomas Simpson became famous for his integration formula which is basically a form of the integration algorithm invented by Johannes Kepler 100 years earlier.
The Simpson formula uses a second order polynomial to approximate a segment of the function to be integrated. Of this polynomial the definite integral can easily be built and computed. The second order polynomial is a very good approximation of a small segment and due to that the result of the Simpson integration is quite useful.
Usually the Simpson integration integrates a function given by some supporting points. It uses a sequence of 3 supporting points y1, y2, y3 to build the polynomial. That means these 3 supporting points build one segment that is integrated at once. Then the next 3 supporting points are taken and integrated in the same manner. This is done in a loop from the beginning till the end of the integration interval. At the end the sum of all these integrals is taken for the result.
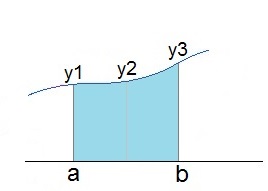
This procedure implies a restriction: There must be an odd number of supporting points.
The segment that should be integrated is b – a = 2h and if a is set to 0 the approximated function f(x) shall be integrated as a function of y1, y2 and y3 like
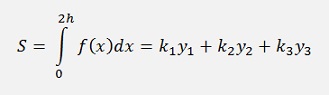
And the factors k1, k2 and k3 shall be determined.
Therefore the formulation for the 3 points y1, y2 and y3 is set up:
With the second order polynomial f(x) is approximated like

This formulation applied for y1, y2 and y3
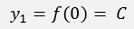
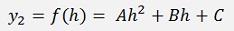
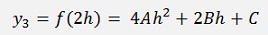
That leads to the equation
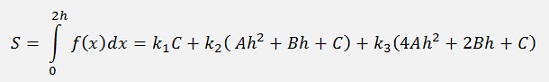
or a bit rearranged
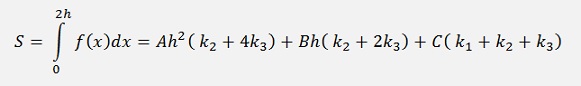
On the other hand

And a parameter comparison leads to the matrix equation:

which can easily be solved and yields
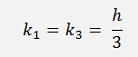

and with this

That’s the integral for one segment. To integrate the entire interval, this formula must be applied in a loop running over the entire integration interval.
With the same sample function I already used or the other integration algorithms:
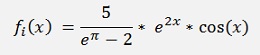
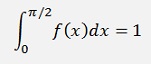
And 7 supporting points like

The loop to compute the Simpson integral looks like:
private double CalcSimpson(int n)
{
int i;
double m;
double h;
h = (b - a) / n;
m = 0;
for (i = 0; i < n-1; i+=2)
{
m = m + f_x(a + h * i)/3 + f_x(a + h * (i+1))*4/3+ f_x(a + h * (i+2))/3;
}
m = m * h;
return m;
}
With
private double f_x(double x)
{
return 5.0 / (Math.Exp(Math.PI) - 2.0) * Math.Exp(2 * x) * Math.Cos(x);
}
With this I get 0.9985. Quite a good accuracy with just 7 supporting points


