Karl Friedrich Gauss (1777 – 1855) was a great mathematician and scientist. I always liked the gentle glance on pictures of him and admired his wisdom.

A picture of him was on a 10 Mark bill of Germany for some time before the Euro came. For sure a beautiful person

The classic approach to solve a matrix equation by Gauss is to eliminate all the elements on the left side of the main diagonal in the matrix and to bring a matrix equation like
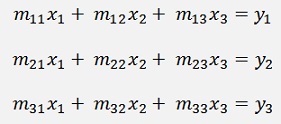
To the form
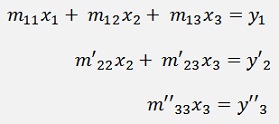
Now the last equation can be solved for x3, with x3 the second equation can be solved for x2 and with x2 and x3 the first equation can be solved for x1 finally. That’s the basic function of the elimination algorithm by Carl Friedrich Gauss. It consists of 2 parts. First the elimination part and second the solving of the equations for the unknown x values.
Elimination
For the elimination procedure we start with the first column elements of the second equation, multiply the second equation by m11 and the first one by m21
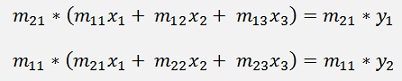
If we subtract the first equation from the second now, we get
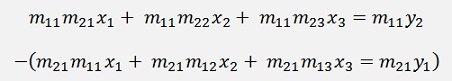
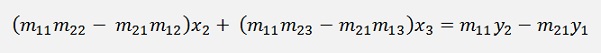
And the first element x1 is eliminated.
For first element of the third equation we do the same: Multiply the third equation by m11 and the first one by m31

And subtract the first one from the third one gives
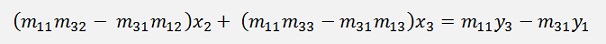
In both equations the first element is eliminated now and we have to eliminate the second element in the third equation. For this we do the same as above again. Multiply the first of those equations by the first element of the second equation and the second equation by the first element of the first equation of those twos and subtract the first from the second.
With the substitution
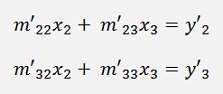
We get
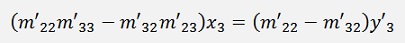
And the second element x2 is eliminated. Finally we are not interested in this numbers. We want to implement this into a loop. With maxOrder as the order of the matrix that looks like:
for (k = 0; k <= maxOrder - 2; k++)
{
for (i = k; i <= maxOrder - 2; i++)
{
for (l = k + 1; l <= maxOrder - 1; l++)
{
m[i + 1, l] = m[i + 1, l] * m[k, k] - m[k, l] * m[i + 1, k];
}
y[i + 1] = y[i + 1] * m[k, k] - y[k] * m[i + 1, k];
m[i + 1, k] = 0;
}
}
Now there are two possible problems:
If m[k,k] = 0 it does not work and if m[i+1,i] = 0 we don’t need to do anything as the element to be eliminated is already 0.
In the first case m[k,k] = 0 the easiest solution is to switch the row k with row k+1. In the second case m[i+1,i] = 0 we could basically say: O.k. who cares. We multiply the first equation by 0 and subtract 0 values from the other equation. Nothing happens and the element to be eliminated is already 0. So nothing happens. That’s an approach of course. But keep in mind: We are working with float values and they become 0 in very rare cases. Most of the time they become almost 0 and calculating with values that are almost 0 costs accuracy and calculation time for nothning. It’s better to do something in this case

So we modify the loop like
for (k = 0; k <= maxOrder - 2; k++)
{
l = k + 1;
while ((Math.Abs(m[k, k]) < 1e-8) && (l < maxOrder))
{
SwitchRows(k);
l++;
}
if (l < maxOrder)
{
for (i = k; i <= maxOrder - 2; i++)
{
if (!calcError)
{
if (Math.Abs(m[i + 1, k]) > 1e-8)
{
for (l = k + 1; l <= maxOrder - 1; l++)
{
m[i + 1, l] = m[i + 1, l] * m[k, k] - m[k, l] * m[i + 1, k];
}
y[i + 1] = y[i + 1] * m[k, k] - y[k] * m[i + 1, k];
m[i + 1, k] = 0;
}
}
}
}
else
calcError = true;
}
void SwitchRows(int n)
{
double tempD;
int i, j;
for (i = n; i <= maxOrder - 2; i++)
{
for (j = 0; j <= maxOrder - 1; j++)
{
tempD = m.a[i, j];
m[i, j] = m[i + 1, j];
m[i + 1, j] = tempD;
}
tempD = m.y[i];
y[i] = y[i + 1];
y[i + 1] = tempD;
}
}
In the switching function I move the row to be switched all the way down to the bottom row. Like this it is possible to do the switching more than one time if necessary. For the switching I put the row that has to be switched to the bottom line and move all other rows up by one line. In case the next row has a 0 in the same element too I switch this one too and so on. But if I have to switch all the rows, the matrix cannot be solved and I have to set a calculation error flag.
With this functions a sample matrix equation

Is brought to the form

And the solution vector becomes

Now there is one great disadvantage of this algorithm. After teh elimination the numbers in the last row are quite big and the result becomes a bit inaccurate because of that.
There are the so called pivoting strategies to improve this behaviour and one of this strategies is to pre-process all the rows first in a way that the sum of all the elements of one row becomes close to 1. That’s what the function Pivot(int n) does:
public void Pivot(int n)
{
double tempD = 0;
int j;
if (n < maxOrder)
{
for (j = 0; j < maxOrder; j++)
{
tempD = tempD + Math.Abs(m[n, j]);
}
tempD = tempD / maxOrder;
if (tempD != 0)
{
for (j = 0; j < maxOrder; j++)
{
m[n, j] = m[n, j] / tempD;
}
y[n] = y[n] / tempD;
}
}
With pivoting after elimination my matrix equation looks like this:

That should do

The impact of the pivoting might not be too clearly visible in the resulting vector on a small matrix equation like here. It becomes effective at matrixes of 8x8 or bigger and even more if the algorithm is running on a 32 bit machine or smaller.
The elimination algorithm of Karl Friedrich Gauss is a nice thing to implement. It’s quite clear regarding it’s function and is easy to understand. But it has its disadvantages: It’s not too accurate and it is a bit sensitive for 0 values in the matrix and range overflows if there is no pivoting. I implemented an algorithm using rotation matrixes for the elimination. This one does not need any pivoting and calculates more accurate. Have a look about that (Rotation Matrix.)
On the other hand the Gaussian elimination algorithm can work with complex numbers as well
I implemented an online Matrix equation solver with the Gaussian elimination algorithm. This Matrix equation solver can be found here


