LU decomposition by Crout and by the use of Frobenius matrixes

LU decomposition by Crout

To solve a matrix equation it is often useful to convert the matrix into a simpler form or parts. An interesting method for this is the LU decomposition by Crout. Its idea is to decompose the matrix M of the matrix equation Mx= y into a lower triangle matrix L and an upper triangle matrix U and write LUx = y. Whereas in the L-matrix all diagonal elements are 1. With these 2 matrixes the equation can be solved in 2 quite simple loops. Therefore Crout introduces another vector y and separates the equation LUx = y into
Lb = y

and

Ux = b

First he calculates the parameters of y and with these he gets the parameters of x which are the solution of the matrix equation. The deduction of these steps is quite a way to go. But it’s worthwhile :-) So let’s start at the beginning.
LU separation

First the matrix A has to be decomposed into this L- and U-matrix: For this we have to start by the multiplication of the 2 matrixes L and U (therefore I use a 4*4 matrix. The result will be valid for n*n matrixes as well)
2x2 Matrix

And comparing it with the originating matrix M
2x2 Matrix


Parameter comparison of the parameters in the first row shows:

u11 = m11
u12 = m12
u13 = m13
u14 = m14


From the first column we get

m21 = u11 * l21
m31 = u11 * l31
m41 = u11 * l41

and resolved for the l parameters

l21 = m21 / u11
l31 = m31 / u11
l41 = m41 / u11


From the second row we take

m22 = u12 * l21 + u22
m23 = u13 * l21 + u23
m24 = u14 * l21 + u24

and resolved for the u parameters

u22 = m22 - u12 * l21
u23 = m23 - u13 * l21
u24 = m24 - u14 * l21


We go on to the second column

m32 = u12 * l31 + u22 * l32
m42 = u12 * l41 + u22 * l42

resolve for the l parameters

l32 = (m32 - u12 * l31) / u22
l42 = (m42 - u12 * l41) / u22


Next is the third row

m33 = u13 * l31 + u23 * l32 + u33
m34 = u14 * l31 + u24 * l32 + u34

here we resolve

u33 = m33 - u13 * l31 - u23 * l32
u34 = m34 - u14 * l31 + u24 * l32


The third column gives

m43 = u13 * l41 + u23 * l42 + u33 * l43

and we get

l43 = (m43 - u13 * l41 - u23 * l42) / u33


And finally

m44 = u14 * l41 + u24 * l42 + u34* l43 + u44

and with this

u44 = m44 - u14 * l41 - u24 * l42 - u34* l43


But how can this be put into an algorithm? If we start at the top row and left column and always calculate the u elements of one row followed by the l elements of one column, it’s not too difficult :-)

If we have a look at the formulas for u, they can be written as

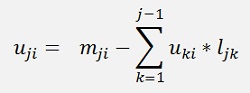
2x2 Matrix
For i >= j

And the formulas for l
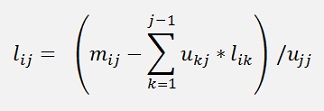
2x2 Matrix
For i > j



And this can be pot into code like

private void LUdecomp()
{
     int i, j, k;
     for (i = 0; i < MaxOrder; i++)
     l[i, i] = 1.0;
    
     for (j = 0; j < MaxOrder; j++)
     {
         for (i = 0; i < MaxOrder; i++)
         {
              if (i >= j)
              {
                   u[j, i] = m[j, i];
                   for(k = 0; k < j; k++)
                        u[j, i] = u[j, i] -  u[k, i] * l[j, k];
              }
              if (i > j)
              {
                   l[i, j] = a[i, j];
                   for(k = 0; k < j; k++)
                        l[i, j] = l[i, j] - u[k, j] * l[i, k];
                   l[i, j] = l[i, j] / u[j, j];
              }
         }
     }
}

This function calculates the two matrixes U and L. Unfortunately we are not done jet.

There is still some math to be survived :-)



Solving the equation

We want to solve a matrix equation and therefore we have to resolve Ly = b
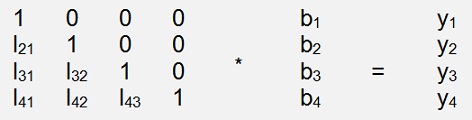
2x2 Matrix

Carrying out this multiplication and a parameter comparison gives:

b1 = b1
b2 = y2 - b1 * l21
b3 = y3 - b1 * l31 – b2 * l32
b4 = y4 - b1 * l41 – b2 * l42 – b3 * l43

The same we have to do for Ux = y now


2x2 Matrix

Here the multiplication and a parameter comparison gives:

x4 = y4 / u44
x3 = (y3 – x4*u34) / u33
x2 = (y2 – x3*u23 – x4*u24) / u22
x1 = (y1 – x2*u12 – x3*u13 – x4*u14) / u11

and the vector x is the solution of our matrix equation.

These 2 sequences can be implemented in 2 loops like

public double[] Solve()
{
     int i, j;
     double[] x = new double[maxOrder];
     for (j = 1; j < maxOrder; j++)
     {
         for (i = 0; i < j; i++)
         {
              y[j] = y[j] - y[i] * l[j, i];
         }
     }
     x[maxOrder - 1] = y[maxOrder - 1] / u[maxOrder - 1, maxOrder - 1];
     for (j = maxOrder - 2; j >= 0; j--)
     {
         x[j] = y[j];
         for (i = maxOrder - 1; i > j; i--)
         {
              x[j] = x[j] - x[i] * u[j, i];
         }
         x[j] = x[j] / u[j, j];
     }
     return x;
}



Now we are almost done. There is only some exception handling missing. There are divisions by ujj in LUdecomp() and in Solve() and ujj can be 0. This has to be handled. Therefore I extended LUdecomp() to return its calculation success as a Boolean type and call Solve() only if this result is true.

Now the solution of our matrix equation is in the vector x.


The LU decomposition is a quite smart approach to solve a matrix equation. In the algorithm of natural splines it’s absolutely superb. (See NaturalSplines.html)



LU decomposition by using Frobenius matrixes

The LU decomposition by Crout has the disadvantage to be sensitive on 0 values in the rows of the main matrix. That can cause the algorithm to quit. Using Frobenius matrixes offer the possibility to switch rows in such a case. That’s quite neat.

A Frobenius matrix is basically an elimination matrix to eliminate the elements below the main diagonal of the column i of a matrix M. A Frobeinius matrix to eliminate the elements of the second column has the form:


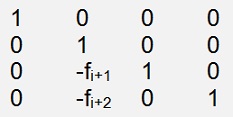
2x2 Matrix


with
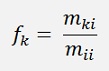
2x2 Matrix


The interesting thing now is that if we transform the matrix A into a right upper triangle matrix by these Frobenius matrixes, the elements of all these Frobenius matrixes used for this transformation can be used to build the left lower triangle matrix in quite a simple way.

With F as the product of all Frobenius matrixes used in the transformation of A into the upper triangle matrix U. We have:
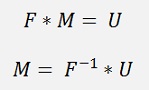
2x2 Matrix


and so
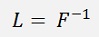
2x2 Matrix


That means the inverse of the product of all Frobenius matrixes is the left lower triangle matrix. On the first glimpse that looks like a lot of calculations. But in fact it isn’t.

If we have a look at the multiplication of F1 whit F2 that’s

 
2x2 Matrix



and that’s
2x2 Matrix


That shows that we just have to add the elements below the main diagonal which are not 0 to the first matrix instead of carrying out a complete multiplication.

The product of all Frobenius matrixes is a lower left triangle matrix containing all the elements below the main diagonal of each matrix that are not 0. That’s quite simple :-)

This matrix has to be inverted now. That’s simple as well. If we just want to invert one Frobenius matrix into a matrix B that would be like

2x2 Matrix



A parameter comparison of the elements in the first row shows

b11 = 1, b12 = 0, b13 = 0 and b14 = 0

That’s not too interesting but o.k.


The second row is quite clear as well:

b21 = 0, b22 = 1, b23 = 0 and b24 = 0


The third row becomes interesting:

b31 = 0


-f32 * b21 + b31 = 0

We already found b21 = 0 and b31 = 0. So that’s o.k.


-f32 * b22 + b32 = 0 As b22 = 1 => b32 = f32


-f32 * b23 + b33 = 1 As b23 = 0 => b33 = 1


-f32 * b24 + b34 = 0 As b24 = 0 => b34 = 0


For the last row we can find:

b41 = 0, b43 = 0 and b44 = 1


and with

-f42 * b22 + b42 = 0 => b42 = f42


That means the inverse matrix looks like

2x2 Matrix





That’s pretty much the same as the origin matrix. Just the sign of the values below the main diagonal have switched. So there is no calculation at all to determine the inverse of F. It’s just switching the sign of the values below the main diagonal and adding them to a starting unit matrix.

Whit this we have all for the LU decomposition and can put it into code like:

 

public void RunFrobenius()
{
     int i, k;
     for (k = 0; k < maxOrder; k++)
     {
         for (i = 0; i < maxOrder - 1; i++)
         {
              l[i, k] = 0.0;
         }
         l[k,k] = 1.0;
     }
     for (i = 0; i < maxOrder; i++)
{
         CalcFMatrix(i);
         MultMatrix(f);
         // copy the values into the L matrix
         for (k = i + 1; k < maxOrder; k++)
              l[k, i] = -f[k, i];
     }
}


With


public void CalcFMatrix(int i)
{
     int j,k ;
     for (j = 0; j < maxOrder; j++)
     {
         for (k = 0; k < maxOrder; k++)
         {
              f[j, k] = 0.0;
         }
         f[j, j] = 1.0;
     }
     for (k = i + 1; k < maxOrder; k++)
     {
         f[k, i] = - m[k,i] / m[i,i];
     }
}



Now this implementation has the same weakness as the algorithm by Crout has it: If there is a matrix like
2x2 Matrix


It would look like


2x2 Matrix



after elimination of the elements in the first column. Now in the second row there is a 0 in the element of the main diagonal. That would cause the algorithm to quit with a calculation error (a division by cero). But here the algorithm using Frobenius matrixes offers the possibility to switch the rows in such a case. If we move the second row to the bottom now, all the problems are solved…If we do it smart :-)

Smart means we have to switch not only the rows of the main matrix and the solution vector but also a part of the same row of the L matrix. There we have to move the elements that we have already determined to the bottom as well.

After eliminating the elements of the first column the L matrix of this sample would look like


2x2 Matrix



And we had to switch only the element f21. Principally only the elements on the left side of the main diagonal of the same row have to be switched. So I implemented the function SwitchRows(..) like




void SwitchRows(int n)
{
     double tempD;
     double tempL;
     int i, j;
     for (i = n; i <= maxOrder - 2; i++)
     {
         for (j = 0; j <= maxOrder - 1; j++)
         {
              // switch rows of main matrix
              tempD = m[i, j];
              m[i, j] = m[i + 1, j];
              m[i + 1, j] = tempD;
              // switch rows of l matrix to
              tempL = l[i, j];
              if (j < n)
              {
                   l[i, j] = l[i + 1, j];
                   l[i + 1, j] = tempL;
              }
         }
         // switch elements of solution vector
         tempD = y[i];
         y[i] = y[i + 1];
         y[i + 1] = tempD;
     }
}

 


and call this function before calculating the Frobenius matrix if the main diagonal element of the actual column is 0.


For the matrixes I use arrays like


public double[,] m;  // main Matrix
public double[] y;   // solution vector
public double[] x;   // vector of the unknowns


And to solve the matrix equation after LU decomposition I use the same function as I did in the algorithm by Crout.

Like that the algorithm works quite well :-)


Some related articles:

  • Cholesky decomposition
  • Householder transformation
  • Singular value decomposition
  • Gram-Schmidt QR decomposition



    • C# Demo Project solving a matrix equation by using the LU decomposation by Crout and Frobenius

  • Matrix_LU.zip
  • Matrix_LR_Frobenius.zip


    • Java Demo Project solving a matrix equation by using the LU decomposation by Crout and Frobenius

  • Matrix_LU.zip
  • MatrixFrobenius.zip