Transposed Matrix

To transpose a matrix means to mirror it at its main diagonal. That switches the number of rows and the number of columns. The main diagonal of a Matrix is the line across the elements c11, c22, c33,..,cnn.
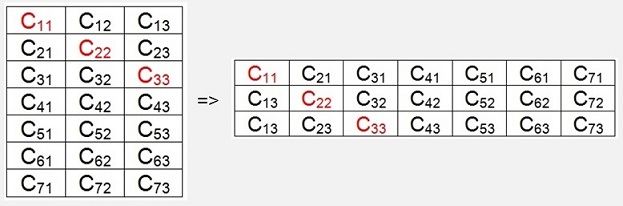
2x2 Matrix




A 7 x 3 matrix and its transposed 3 x 7 matrix.

Now there is one calculation rule for transposed Matrixes which is essential for the derivation of the method of the least squares in approximation. That’s why I want to introduce it:
Associative law for transposed Matrixes

The associative law for transposed Matrixes says the product of 2 transposed Matrixes is equal to the transposed product of the not transposed Matrixes in switched order.
AT * BT  =  (B * A)T


To prove that we first carry out the multiplication of this two transposed Matrixes:


AT * BT  =

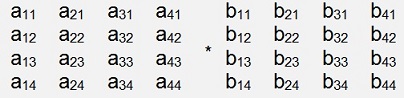
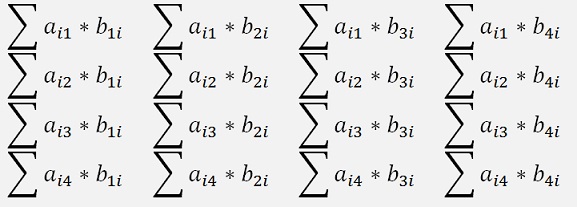
2x2 Matrix

=

2x2 Matrix

Now we multiply the two switched Matrixes

B * A  = 

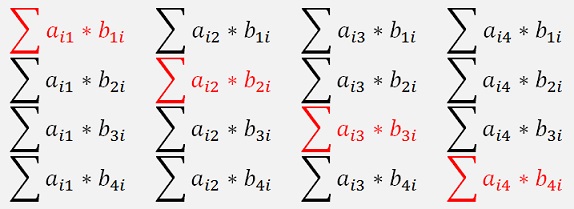
2x2 Matrix

=

2x2 Matrix

This we transpose

(B * A )T =

2x2 Matrix



and can see
AT * BT  =  (B * A)T



And from this we also get
A * BT  =  (B * AT)T



The same is valid for two N*N Matrixes.
Multiplication of A * AT

The multiplication of a Matrix with its transposed is a special case too. The result of this multiplication is a symmetric Matrix
A * AT=

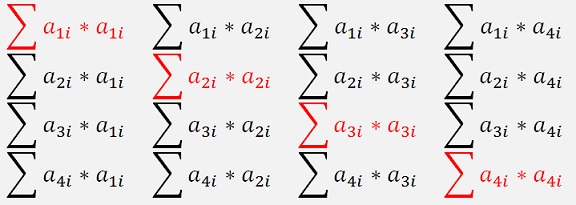
2x2 Matrix
=
2x2 Matrix

The resulting Matrix is Symmetrical to the main diagonal.

The same is valid for a N * N Matrix.