If a function with 2 input variables is differentiable, it’s derivation with respect to one variable is defined like:

This is called partial derivative and can generally be written for a function of variables x1…xn:
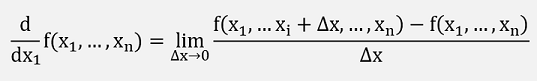
Of course, a derivation is not written like this. It is carried out in the same manner as the derivation of a function with just one variable is done (see Differential calculus). Only all the other variables in the function are regarded as constant for the derivation and this is done with respect to each included variable.For instance for the function
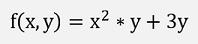
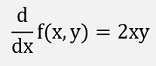
and
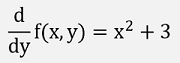
Gradient
All partial derivatives combined in one vector build the Gradient which is usually indicated by the Nabla-operator ∇:
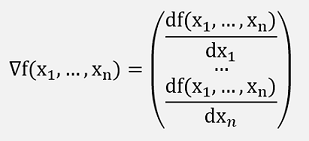
Directional derivative
The directional derivative should not get mixed up with the Gradient. The directional derivative adds the derivations with respect to each variable multiplied by a unit vector pointing into a certain direction. Its result is a single value.
With the unit vector a, that would look like:
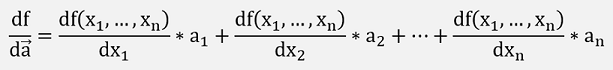
Hessian Matrix
If the function f(x1…xn) can be differentiated twice and all second derivatives are built, we get the Hessian Matrix:
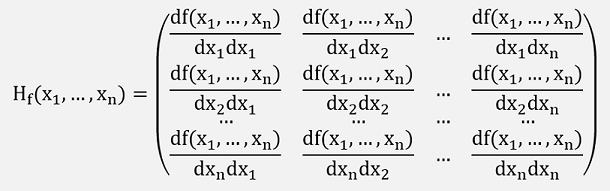
The Hessian matrix is symmetrical to the main diagonal as
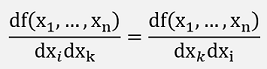
Taylor's theorem
According to Taylor each n times differentiable function can be expressed as a polynomial function at a place x0 plus remainder F(a):
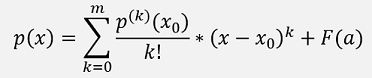
where
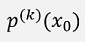
Is the k-th derivation of p at the place x0.
(see Taylor Polynomials)
This formulation can be extended to functions with more than one variable as well.
For a function with 2 variables x and y that means we have to replace
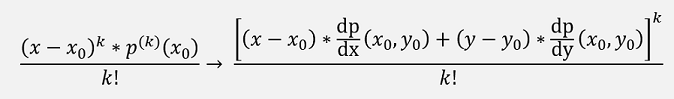
For instance, for k = 2 that would be:
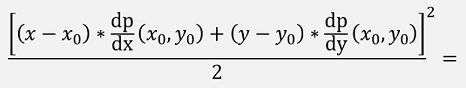
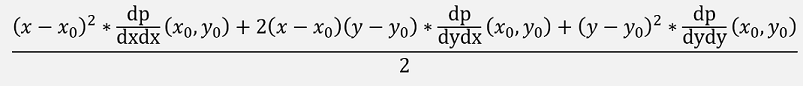
Now, as
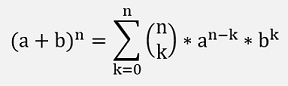
With the Binominal coefficients
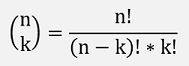
We can write
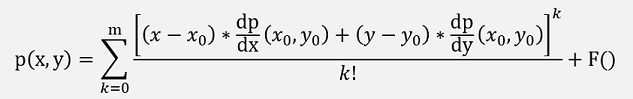
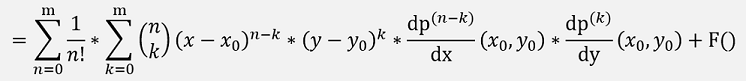
With the remainder:
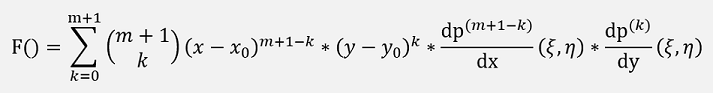
With (ξ,η) a not known point between (x0,y0) and (x,y)
If, for instance, the function
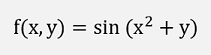
With (ξ,η) a not known point between (x0,y0) and (x,y) shall be approximated at the point x = 0.3 and y = 0.3 by the Taylor function built an the position x0 = 0 and y0 = 0, the first derivations are:

and the second:
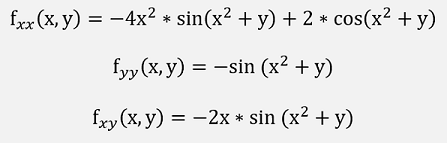
With these the approximation becomes:
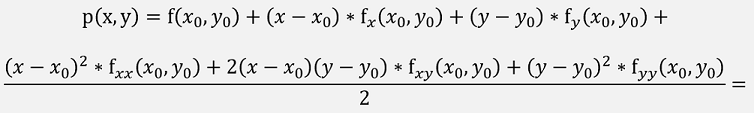

Whereas the origin function:
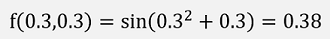
For a function with n variables things become really complicate

Let’s leave that like this

If m = 2, the Tailor polynomial is the quadratic approximation of p.
With the direction vector
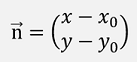
the Gradient of f
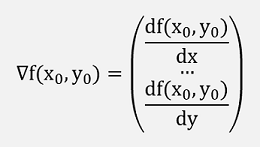
and the Hessian matrix
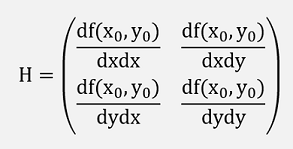
The formulation for the quadratic approximation can be written as:
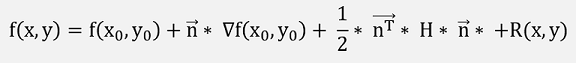
A formulation often mentioned in books about machine learning which looks a bit simpler with a few Matrix operations and it can easily be extended to n variables


