Today a 64 bit processor with the most programming languages is capable to compute calculations with an accuracy of 15 decimal places. That’s quite accurate. But if we need more, we have to implement that by ourselves. I wanted to compute π with more accuracy and so I started this interesting adventure to implement a library to compute calculations with an random number of decimal places.

Such a library must first of all contain the basic operations +, -, *, /. So I started with the easiest operation: The addition of two numbers:

To add two numbers the basic procedure is to start on the right side and to add the numbers column wise. If the addition result becomes >= 10, the part that is >= 10 is transferred to the next column to the left.

For instance:

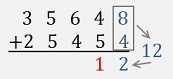
Here the first column on the very right 8 + 4 = 12. The 12 is separated into 2 and 10. The 10 is transferred as 1 to the next column.

The next column 6 + 5 + 1 is 12 again. So, again the 10 is transferred to the next column to the left and so on. Until we get:

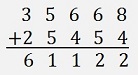
The transferring of the numbers >= 10 does not have to be done column wise. It can be left till all columns are added. We can first add all columns like:get:

And then start on the right side and transfer each part >= 10 to the next number to the left.

Do this for all columns

That’s quite easy.

There is only one special case: In case the column value on the very left is >= 10, the resulting number gets one column more.

To handle numbers with an arbitrary number of decimal places, I implemented a number as a class carrying the value of the number in an array with a sign and an exponent like:

class ExtFloat
{
     private int decplaces = 150;
     public int[] value;
     public int sign;
     public int exp;
}

This number has just one single digit above the floating point. A number like 1503 would be 1.503E3 and 0.00353 would be 3.53E-3.

In this class I implemented the basic operations. The basic addition of two positive numbers like this (with equal exponent) would be:

private static ExtFloat BasicAdd(ExtFloat aL, ExtFloat bL)
{
     // Add a positive number to a positive number
     int i, j;
     ExtFloat result = new ExtFloat();
     int tempD;
     j = 0;
 
     result.exp = aL.exp;
     for (i = 0; i < aL.value.Length; i++)
     {
         result.value[i] = aL.value[i] + bL.value[i];
     }
     for (j = result.value.Length - 1; j > 0; j--)
     {
         if (result.value[j] >= 10)
         {
              tempD = result.value[j] - (result.value[j] / 10) * 10;
              result.value[j - 1] += result.value[j] / 10;
              result.value[j] = tempD;
         }
     }
     if (result.value[0] >= 10)
     {
         tempD = result.value[0] / 10;
         result.value[0] = result.value[0] - (result.value[0] / 10) * 10;
         for (j = result.value.Length - 1; j > 0; j--)
         {
              result.value[j] = result.value[j - 1];
         }
     result.value[0] = tempD;
     result.exp++;
     }
     return result;
}

It adds two positive numbers with equal exponent.



The next step is the subtraction of one number from another like:

The procedure here is a bit different from the addition. It starts on the left side:

Now the next column to the right becomes negative

That means we have to transfer -10 as a -1 to the next column to the left and in the second column 9 remains:

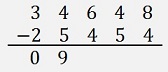
The next column is 2

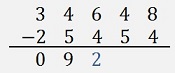
Then we get -1 again

That makes

And with the last column, that becomes 4. And we are done.

It would be easy the handle the subtraction similar to an addition. But there is one little complication: If the result becomes negative everything becomes different.

For instance:

It’s no more just the number above minus the number below. This situation must be handled in a different way.

The solution is quite simple: Just switch the sign of all 3 numbers and go on subtracting . But the decision whether the result becomes negative or not is not that simple. It must be done for the first value that is not 0 and becomes negative only. Due to this the function BasicSubtract becomes a bit more complex:

private static ExtFloat BasicSubtract(ExtFloat aL, ExtFloat bL, bool withExp = true)
{
     // Subtract a positive number from a positive number
     int i, j;
     ExtFloat result = new ExtFloat();
     int tempD;
     bool isZero = true;
     j = 0;
 
     result.exp = aL.exp;
     for (i = 0; i < aL.value.Length; i++)
     {
         tempD = (aL.value[i] * aL.sign) - (bL.value[i] * bL.sign);
         if (tempD >= 0)
         {
              result.value[i] = tempD;
              if (tempD > 0)
                   isZero = false;
         }
         else
         {
              if (i > 0)
              {
                   if (!isZero)
                   {
                        result.value[i] = 10 + tempD;
                        result.value[i - 1] -= 1;
                   }
                   else
                   {
                        result.value[i] = -tempD;
                        if (result.value[i] > 0)
                            isZero = false;
                        result.sign = -1;
                        aL.sign = -1;
                        bL.sign = -1;
                   }
              }
              else
              {
                   result.value[i] = -tempD;
                   if (result.value[i] > 0)
                        isZero = false;
                   result.sign = -1;
                   aL.sign = -1;
                   bL.sign = -1;
              }
         }
     }
     for (j = result.value.Length - 1; j > 0; j--)
     {
         if (result.value[j] < 0)
         {
              tempD = result.value[j];
              result.value[j - 1] -= 1;
              result.value[j] = tempD + 10;
         }
     }
     return result;
}

Now these two functions BasicAdd() and BasicSubtract() work only with two positive numbers with the same exponent. If one of these numbers is negative or has another exponent that must be handled before these functions can be used. Therefore these functions are private and there are two public functions that handle these things.

The public function for an addition looks like:

public static ExtFloat Add(ExtFloat aIn, ExtFloat bIn)
{
     int j;
     int order = aIn.value.Length;
     ExtFloat aL = new ExtFloat(aIn);
     ExtFloat bL = new ExtFloat(bIn);
     ExtFloat a2 = new ExtFloat();
     ExtFloat result = new ExtFloat();
     int tempD;
     j = 0;
 
     if (aL.exp > bL.exp)
         bL = MoveExp(bL, aL.exp - bL.exp);
     else
     {
         if (bL.exp > aL.exp)
              aL = MoveExp(aL, bL.exp - aL.exp);
     }
     result.exp = aL.exp;
     if (aL.sign > 0)
     {
         if (bL.sign > 0)
         {
              result = BasicAdd(aL, bL);
         }
         else
         {
              bL.sign = 1;
              result = BasicSubtract(aL, bL);
         }
     }
     else
     {
         aL.sign = 1;
         if (bL.sign > 0)
         {
              result = BasicSubtract(bL, aL);
         }
         else
         {
              bL.sign = 1;
              result = BasicAdd(bL, aL);
              result.sign = -result.sign;
         }
 
     }
     for (j = result.value.Length - 1; j >= 1; j--)
     {
         if (result.value[j] >= 10)
         {
              tempD = result.value[j] - 10;
              result.value[j - 1] += 1;
              result.value[j] = tempD;
         }
     }
     if (result.value[0] >= 10)
     {
         tempD = result.value[0] / 10;
         result.value[0] = result.value[0] - tempD * 10;
         for (j = result.value.Length - 1; j >= 1; j--)
         {
              result.value[j] = result.value[j - 1];
         }
         result.value[0] = tempD;
         result.exp++;
     }
     return result;
}

This function equalizes the exponent of both numbers, checks the sign of both and handles them by adding or subtracting the numbers accordingly


The function MoveExp() is used to equalize the exponents of both numbers. It moves the floating point of an ExtFloat by a number of places to the left, fills the inserted place with 0’s and increases the exponent by the same number.

private static ExtFloat MoveExp(ExtFloat a, int number)
{
     int i, j;
     for (i = 0; i < number; i++)
     {
         for (j = a.value.Length - 1; j > 0; j--)
              a.value[j] = a.value[j - 1];
         a.value[0] = 0;
     }
     a.exp += number;
     return a;
}

The subtracting function is quite similar:

public static ExtFloat Subtract(ExtFloat aIn, ExtFloat bIn)
{
     int i, j;
     ExtFloat result = new ExtFloat();
     ExtFloat aL = new ExtFloat(aIn);
     ExtFloat bL = new ExtFloat(bIn);
     j = 0;
 
     if (aL.exp > bL.exp)
         bL = MoveExp(bL, aL.exp - bL.exp);
     else
     {
         if (bL.exp > aL.exp)
              aL = MoveExp(aL, bL.exp - aL.exp);
     }
     result.exp = aL.exp;
     if (aL.sign > 0)
     {
         if (bL.sign > 0)
         {
              result = BasicSubtract(aL, bL);
         }
         else
         {
              bL.sign = 1;
              result = BasicAdd(aL, bL);
         }
     }
     else
     {
         aL.sign = 1;
         if (bL.sign > 0)
         {
              result = BasicAdd(aL, bL);
              result.sign = -result.sign;
         }
         else
         {
              bL.sign = 1;
              result = BasicSubtract(bL, aL);
         }
 
     }
     j = 0;
     while ((result.value[0] == 0) && (j < result.value.Length))
     {
         for (i = 0; i < result.value.Length - 1; i++)
         {
              result.value[i] = result.value[i + 1];
         }
         j++;
         result.exp--;
     }
     return result;
}

At the end of this function the result could look like 0.000451.. The function makes of that 4.51… and sets the exponent accordingly.


The next a bit more complicate operation is the multiplication of two numbers. The procedure for this, for instance for the multiplication of 52317 * 56. is:

First multiply 52317 * 5 and keep the result. Then multiply 52317 * 6, shift the result by one column to the right and add it to the multiplication of 52317 * 5

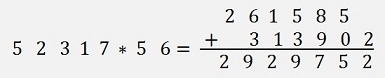
The addition can be done by the function already implemented.

public static ExtFloat Mult(ExtFloat aIn, ExtFloat bIn)
{
     ExtFloat aL = new ExtFloat(aIn);
     ExtFloat bL = new ExtFloat(bIn);
     ExtFloat result = new ExtFloat();
     ExtFloat a2 = new ExtFloat();
     int i, j, k;
     int tempD;
 
     for (k = 0; k < bL.value.Length; k++)
     {
         for (i = 0; i < a2.value.Length; i++)
              a2.value[i] = 0;
         a2.exp = 0;
         if (bL.value[k] > 0)
         {
              for (i = 0; i < bL.value.Length; i++)
              {
                   if ((k + i) < bL.value.Length)
                   {
                        a2.value[k + i] = aL.value[i] * bL.value[k];
                   }
              }
              for (i = aL.value.Length - 1; i > 0; i--)
              {
                   if (a2.value[i] >= 10)
                   {
                        tempD = a2.value[i] / 10;
                        a2.value[i - 1] += tempD;
                        a2.value[i] = a2.value[i] - tempD * 10;
                   }
              }
              if (a2.value[0] > 10)
              {
                   for (i = aL.value.Length - 1; i > 0; i--)
                   {
                        a2.value[i] = a2.value[i - 1];
                   }
                   tempD = a2.value[0] / 10;
                   a2.value[0] = tempD;
                   a2.value[1] = a2.value[1] - tempD * 10;
                   a2.exp++;
              }
              result = Add(result, a2);
         }
     }
     result.exp += aL.exp + bL.exp;
     result.sign = aL.sign * bL.sign;
     j = 0;
     while ((result.value[0] == 0) && (j < result.value.Length))
     {
         for (i = 0; i < result.value.Length - 1; i++)
         {
              result.value[i] = result.value[i + 1];
         }
         j++;
         result.exp--;
     }
     if (result.value[0] >= 10)
     {
         tempD = result.value[0] / 10;
         result.value[0] = result.value[0] - tempD * 10;
         for (j = result.value.Length - 1; j >= 1; j--)
         {
              result.value[j] = result.value[j - 1];
         }
         result.value[0] = tempD;
         result.exp++;
     }
     return result;
}
.

There is the same here: If one number becomes >= 10 that must be handled and at the end the first number must be checked if it is >= 10 and that must be handled as well



The highest discipline of the standard operations is the division of one number by another

The basic procedure for this division is:

Take as many digits of 2929752 as has 52317. That would be 29297.

Check how many times 52317 can be subtracted from this 29297. That’s 0 here.

In this case take as many digits of 2929752 as has 52317 plus 1.

Check how many times 52317 can be subtracted from this 292975. That’s 5 times now and 52317 * 5 = 261585. Subtract this 261585 from 292975 and 5 is the first digit of the result..

There remains 31390. Add the last digit of 2929752 and put it at the end of 31390. That gives 313902.

Check how many times 313902 can be subtracted from this 29297. That’s 6 times. That’s the second digit of the result.


This function looks like:

public static ExtFloat Divide(ExtFloat aIn, ExtFloat bIn)
{
     int i, j, k;
     int actPlace = 0;
     ExtFloat aL = new ExtFloat(aIn);
     ExtFloat bL = new ExtFloat(bIn);
     ExtFloat a2 = new ExtFloat();
     ExtFloat result = new ExtFloat();
 
     if (Cmp(bL, result) != 0)
     {
         result.sign = aL.sign * bL.sign;
         aL.sign = 1;
         bL.sign = 1;
         for (k = 0; k < aIn.value.Length; k++)
         {
              a2.value[0] = aL.value[0];
              j = 0;
              for (i = 0; i < aIn.value.Length; i++)
              {
                   a2.value[i] = aL.value[i];
              }
              while (CmpNum(a2, bL) >= 0)
              {
                   a2 = BasicSubtract(a2, bL);
                   j++;
              }
              result.value[actPlace] = j;
              actPlace++;
              for (i = 0; i < aIn.value.Length - 1; i++)
              {
                   aL.value[i] = a2.value[i + 1];
              }
              aL.value[i] = 0;
              if (a2.value[0] != 0)
                   aL.value[0] += a2.value[0] * 10;
         }
         result.exp = aL.exp - bL.exp;
     }
     else
     {
         throw new DivideByZeroException();
     }
     j = 0;
     while ((result.value[0] == 0) && (j < result.value.Length))
     {
         for (i = 0; i < result.value.Length - 1; i++)
         {
              result.value[i] = result.value[i + 1];
         }
         j++;
         result.exp--;
     }
     return result;
}

The function CmpNum() compares only the value without considering the exponent and for the subtraction the function BasicSubtract() can be used.


With these functions the standard operations are implemented. For convenience I overload the standard operators with: be

public static ExtFloat operator +(ExtFloat a, ExtFloat b)
{
     return Add(a, b);
}
 
public static ExtFloat operator -(ExtFloat a, ExtFloat b)
{
     return Subtract(a, b);
}
 
public static ExtFloat operator *(ExtFloat a, ExtFloat b)
{
     return Mult(a, b);
}
 
public static ExtFloat operator /(ExtFloat a, ExtFloat b)
{
     return Divide(a, b);
}

Now, to implement only the standard operations is possibly not too interesting. There are some more functions needed for a useful library. So, let’s try the function Pow(). The Pow() function is not too complicate (at least as long as the exponent is an integer):

public static ExtFloat Pow(ExtFloat radiant, int exp)
{
     ExtFloat result = new ExtFloat(1);
     int i;
     for (i = 0; i < exp; i++)
         result = result * radiant;
     return result;
}

To compute the root of a number is already a bit more sophisticated. It can be done by the algorithm introduced in Computing a random root of a number. Only all the variables used must be implemented as ExtFloat types.

public static ExtFloat Root(ExtFloat radiant, int exp)
{
     int i, j;
     ExtFloat x = new ExtFloat();
     ExtFloat tempN = new ExtFloat();
     ExtFloat one = new ExtFloat(1);
     ExtFloat zero = new ExtFloat();
     ExtFloat DELTA = new ExtFloat(StrToNumber("1E-120"));
     ExtFloat x_old = new ExtFloat(radiant);
     ExtFloat x_new = new ExtFloat(radiant);
     ExtFloat extExp = new ExtFloat(exp);
     bool run = true;
     int count = 0;
     if (exp > 1)
     {
         while (run && (count < 1000))
         {
              CopyTo(x_old, x_new);
              for (i = 1; i < exp - 1; i++)
                   x_new = x_new * x_old;
              tempN = (radiant - (x_new * x_old)) / extExp / x_new;
              x = x_old + tempN;
              run = Cmp(Abs(x_old - x), DELTA) > 0;
              CopyTo(x, x_old);
              count++;
         }
         if (count >= 1000)
              x = IntToNumber(0);
     }
     else
     {
         if (exp == 1)
              x = radiant;
         else
         {
              if (exp < 0)
              {
                   x = Root(radiant, -exp);
                   if (ExtFloat.Cmp(x, zero) != 0)
                        x = one / x;
              }
              else // exp is 0
                   x = one;
         }
     }
     j = 0;
     while ((x.value[0] == 0) && (j < x.value.Length))
     {
         for (i = 0; i < x.value.Length - 1; i++)
         {
              x.value[i] = x.value[i + 1];
         }
         j++;
         x.exp--;
     }
     return x;
}

This function computes roots wits an integer value as exponent and if the exponent is negative if returns 1 / Root() (that means it is recursive with one recursion). The function CopyTo() is used like a “=” is copies the value including sign and exp to another number.


One step more is the Sin(x) function. The function Sin(x) can be computed by a Taylor polynomial (see Approximation by Taylor polynomials ). It looks like:

public static ExtFloat Sin(ExtFloat x)
{
     ExtFloat MinusPi = new ExtFloat(Pi);
     MinusPi.sign = -1;
     ExtFloat result = new ExtFloat();
     ExtFloat tempX = new ExtFloat();
     ExtFloat k = new ExtFloat();
     ExtFloat fact = new ExtFloat(1);
     int i= 1;
     int j;
 
     if (Cmp(x, Pi) > 1)
     {
         while (Cmp(x, Pi) > 0)
         {
              x = x - Pi;
              i++;
         }
     }
     else
     {
         while (Cmp(x, MinusPi) < 0)
         {
              x = x + Pi;
              i++;
         }
     }
     if (i % 2 != 0)
         x.sign *= -1;
     for (i = 1; i < 80; i++)
     {
         fact.InitInt(1);
         for (j = (2 * i - 1); j > 1; j--)
         {
              k.InitInt(j);
              fact = fact * k;
         }
         if (i % 2 == 0)
              result = result - Pow(x, 2 * i - 1) / fact;
         else
              result = result + Pow(x, 2 * i - 1) / fact;
     }
     return result;
}

And the Cosine function is similar:

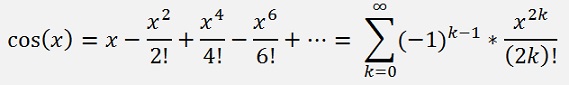
The function as well

public static ExtFloat Cos(ExtFloat x)
{
     ExtFloat MinusPi = new ExtFloat(Pi);
     MinusPi.sign = -1;
     ExtFloat result = new ExtFloat(1);
     ExtFloat tempX = new ExtFloat();
     ExtFloat k = new ExtFloat();
     ExtFloat fact = new ExtFloat(1);
     int i = 1;
     int j;
 
     if (Cmp(x, Pi) > 1)
     {
         while (Cmp(x, Pi) > 0)
         {
              x = x - Pi;
              i++;
         }
     }
     else
     {
         while (Cmp(x, MinusPi) < 0)
         {
              x = x + Pi;
              i++;
         }
     }
     if (i % 2 != 0)
         x.sign *= -1;
     for (i = 1; i < 80; i++)
     {
         fact.InitInt(1);
         for (j = (2 * i); j > 1; j--)
         {
              k.InitInt(j);
              fact = fact * k;
         }
         if (i % 2 == 0)
              result = result + Pow(x, 2 * i) / fact;
         else
              result = result - Pow(x, 2 * i) / fact;
     }
     return result;
}

Both functions sin(x) and cos(x) are defined for values ± 2π. From any Value bigger than π, π should be subtracted and if π had to be subtracted odd times, the sign of x must be changed.


The exponential function can be computed by a Taylor polynomial to:

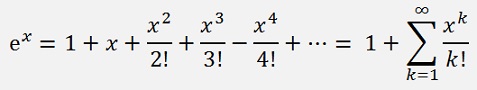
That’s quite a small function:

public static ExtFloat Exp(ExtFloat x)
{
     ExtFloat one = new ExtFloat(1);
     ExtFloat two = new ExtFloat(2);
     ExtFloat result = new ExtFloat(one);
     ExtFloat denominator = new ExtFloat();
     ExtFloat enumerator = new ExtFloat();
     ExtFloat fact = new ExtFloat(one);
     int i;
    
     denominator = one;
     enumerator = one;
     for (i = 1; i < 80; i++)
     {
         enumerator = enumerator * x;
         denominator = denominator * fact;
         fact = fact + one;
         result = result + enumerator/ denominator;
     }
     return result;
}

The counterpart to the exponential function is the logarithm function. It can be implemented as a Taylor polynomial as well:

public static ExtFloat Ln(ExtFloat x)
{
     ExtFloat zero = new ExtFloat();
     ExtFloat one = new ExtFloat(1);
     ExtFloat two = new ExtFloat(2);
     ExtFloat res = new ExtFloat(0);
     ExtFloat result = new ExtFloat();
     ExtFloat denominator = new ExtFloat();
     ExtFloat enumerator = new ExtFloat();
     ExtFloat fact = new ExtFloat(one);
     ExtFloat expX = new ExtFloat(x);
     int i = 0;    
 
     expX = Exp(one);
     while (Cmp(x, expX) > 0)
     {
         x = x / expX;
         res = res + one;
     }
 
     ExtFloat enumfact = new ExtFloat(x - one);
     ExtFloat denomfact = new ExtFloat(x + one);
 
     if (Cmp(x, zero) > 0)
     {
         enumerator = x - one;
         denominator = x + one;
         for (i = 1; i < 500; i += 2)
         {
              result = result + (enumerator / denominator) / fact;
              enumerator = enumerator * enumfact * enumfact;
              denominator = denominator * denomfact * denomfact;
              fact = fact + two;
         }
         result = result * two;
     }
     result = result + res;
     return result;
}

I implemented some convenience functions to:

An ExtFloat variable can be initialized with an integer value or another ExtFloat variable. If there is need for the initialization of an ExtFloat with a float value, that can be done by the usage of the function StrToNumber(). This function interprets the input string as a float value, initializes a ExtFloat variable with that and returns this.

ExtFloat DELTA = new ExtFloat(ExtFloat.StrToNumber("1E-141"));

This line initializes the variable DELTA with the value = 1 and exp = -141.


For the conversation into a string that can be displayed there is the function

public string NumberToStr(int fractionPlaces)

public string NumberToStr()

public static void CopyTo(ExtFloat a, ExtFloat b)

 

That copies the values of a into b.

An Abs() function is implemented as well. It creates an new instance of a ExtFloat and returns that with positive sign.

The function Round(int fractionPlaces) need not to be explained I think

A Cmp(ExtFloat aIn, ExtFloat bIn) is impelented in two ways. First the function

public static int Cmp(ExtFloat aIn, ExtFloat bIn)

compares two ExtFloat variables and returns

 1 if aIn > bIn
 0 if aIn == bIn
-1 if aIn < bIn


The function

private static int CmpNum(ExtFloat aIn, ExtFloat bIn)

does basically the same. But it only considers the value without the exponent. I need this function in the Divide() function. Therefore it is private.


With this the ExtFloat library is complete for the moment. I used a part of this library to compute π with up to 1000 decimal places (see Computing Pi)



The demo project consists of one main window

C# Demo Project ExtFloat Test