Angle addition theorems are quite useful if it come to reforming equations. Most often they are just written without any explanation or derivation. Therefore I tried to do this for some of them.
The first and maybe most important theorem is the theorem of Pythagoras applied to angular functions

This can be reformed to:
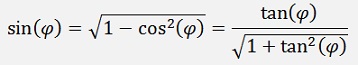
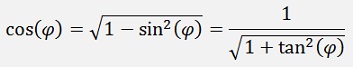
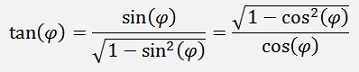

A complex number has a length (r), a real part (a), an imaginary part (ib) and an angle φ.

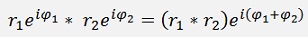
In absolute size the multiplication looks like:
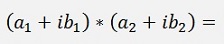

(See Complex numbers)
The length r of this multiplication becomes:
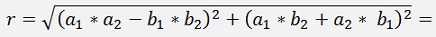

Which can be reformed to
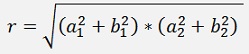
and the sinus of the new angle is the imaginary part divided by the length.
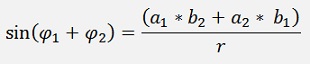
with
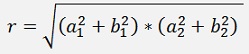
Disassembled
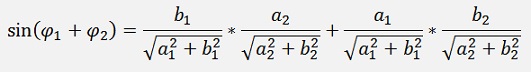
and as

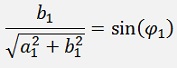
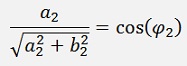
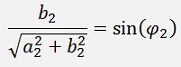
we get

or

In the same manner one can say for the cosine function:
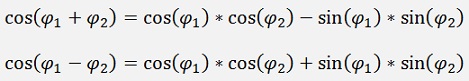
And for the tangent function we can use both of the above formulas:
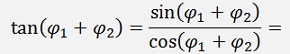
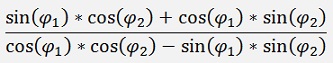
The denominator of this fraction can be written as:
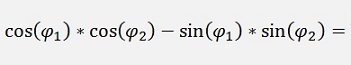

And the two parts of the numerator

These parts in the above formulation:
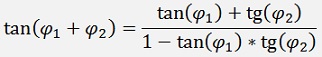
or
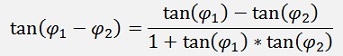
The multiplication of 2 angles like:
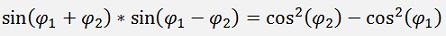
Can be derived by the above formulas
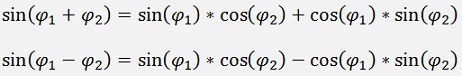
Both multiplied we get:
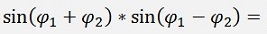

and with Pythagoras:
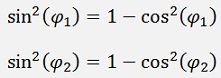




And in the same manner:
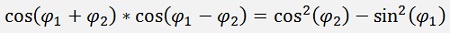
For functions with doubled angles the above formulas can be used:
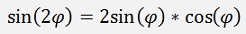

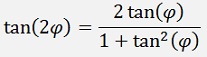
For functions with half angles like:
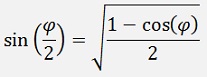
The formula for double angles is used:

And from Pythagoras
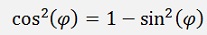
We can rewrite
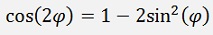
and
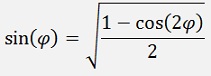
The angle divided by 2 means:
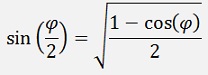
And in the same manner:

The addition of 2 sinuses
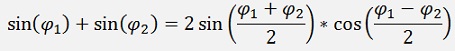
with

and
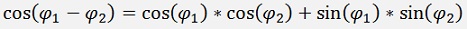
Multiplied



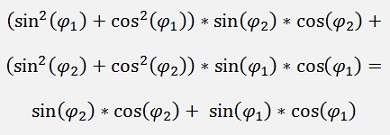
And with
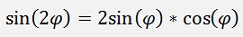

Or with the half angles and reformed:

And in the same manner:
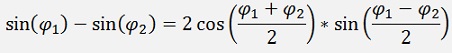
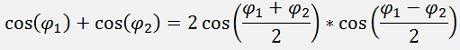
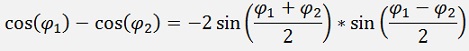
That should do for the moment


