A band filter can be derived from a low pass filter by a so called low pass to band pass or band stop transformation. In this article I did this transformations with the filter algorithm of the Butterworth filter

The low pass to band pass transformation is quite similar to a low pass to high pass transformation. In the transfer function of the low pass filter

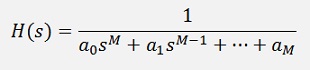
The Laplace variable s must be substituted:

With ΔΩ the normalized frequency gap of the band, s_lp is s of the origin low pass filter and s_bp is the s of the band pass filter

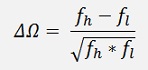
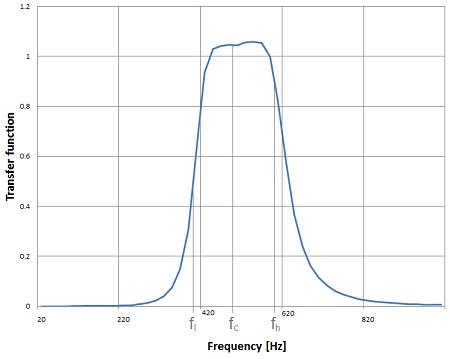
In this graph f_c is the cut of off frequency of the origin low pass filter. The pass band filter transformation mirrors the low pass filter to an additional high pass filter and shifts the frequency of both filters by the half of the filter band.

That means in the transfer function

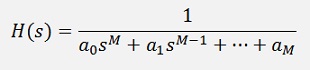
Every s must be replaced by

Written in a generalized form that’s

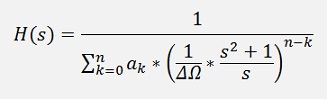
The fraction in the denominator must be eliminated:

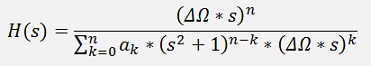
That would look like

public void BandFilterTransformation()
{
     int i, j;
     double[] tempA = { 1.0, 0, 1.0 }; // s^2 + 1
     double[] tempB = { deltaOmega, 0 }; // s * deltaOmega
     List<double[]> bandPar = new List<double[]>();
 
     for (i = 0; i <= order; i++)
     {
         double[] tempEl = Poly.Mult(Poly.Power(tempA, order - i), Poly.Power(tempB, i));
         tempEl = Poly.Mult(tempEl, a_s[i]);
         bandPar.Insert(i, tempEl);
     }
     Array.Resize(ref a_s, bandPar.ElementAt(0).Length);
     for (i = 0; i < a_s.Length; i++)
     {
         a_s[a_s.Length - 1 - i] = 0;
         for (j = 0; j < bandPar.Count; j++)
         {
              if (i < bandPar.ElementAt(j).Length)
                   a_s[a_s.Length - 1 - i] = a_s[a_s.Length - 1 - i] + bandPar.ElementAt(j)[bandPar.ElementAt(j).Length - 1 - i];
         }
     }
     b_s = Poly.Mult(b_s, tempB);
     b_s = Poly.Power(b_s, order);
}

This function converts a given transfer function of a low pass filter, which is in the arrays a_s and b_s into a transfer function of a band pass filter and puts it back into the arrays a_s and b_s. In the complete algorithm first the Butterworth filter parameters must be computed and then these parameter are transformed into the band pass parameters..


In the graph of the transfer function further above one can see that the curve is not symmetrical to f_c. I regard this as a weakness of this algorithm. It’s not symmetrical to f_c and the wider the band f_h – f_l the more asymmetrical it becomes. That means the less steep the slope on the side of f_h will be. The algorithm works quite well for very narrow pass bands. For wider pass bands its smarter to combine a ordinary low pass filter with a high pass filter to implement the band pass filter.


With this we get the transfer function for the band pass filter in the Laplace domain. An important detail is that, if we start with a low pass filter of the order = N, the band pass filter gets the order = 2N.

This transfer function must be transferred to the z-domain now. That’s similar to how I did it in Butterworth filter

public void TransformToZPlane()
{
     int i, j;
     double[] tempA = new double[2];
     List<double[]> aa = new List<double[]>();
     List<double[]> bb = new List<double[]>();
 
     for (i = 0; i < a_s.Length; i++)
     {
         aa.Add(new double[] { 1, -1 });
     }
     for (i = 0; i < b_s.Length; i++)
     {
         bb.Add(new double[] { 1, -1 });
     }
     tempA[0] = 1;
     tempA[1] = 1;
     for (i = 0; i < a_s.Length; i++)
     {
         double[] tempEl = aa.ElementAt(i);
         tempEl = Poly.Mult(Poly.Power(tempA, i), Poly.Power(tempEl, a_s.Length - 1 - i));
         tempEl = Poly.Mult(tempEl, a_s[i] * Math.Pow(2.0 / tc, a_s.Length - 1 - i));
         aa.RemoveAt(i);
         aa.Insert(i, tempEl);
     }
 
     for (i = 0; i < b_s.Length; i++)
     {
         double[] tempEl = bb.ElementAt(i);
         tempEl = Poly.Mult(Poly.Power(tempA, i), Poly.Power(tempEl, b_s.Length - 1 - i));
         tempEl = Poly.Mult(tempEl, b_s[i] * Math.Pow(2.0 / tc, b_s.Length - 1 - i));
         bb.RemoveAt(i);
         bb.Insert(i, tempEl);
     }
 
     a_z = new double[aa.Count];
     for (i = 0; i < a_z.Length; i++)
     {
         a_z[i] = 0;
         for (j = 0; j < aa.Count; j++)
         a_z[i] = a_z[i] + aa.ElementAt(j)[i];
     }
 
     b_z = new double[bb.Count];
     for (i = 0; i < b_z.Length; i++)
     {
         b_z[i] = 0;
         for (j = 0; j < bb.Count; j++)
         b_z[i] = b_z[i] + bb.ElementAt(j)[i];
     }
 
     for (i = 0; i < b_z.Length; i++)
     {
         b_z[i] = b_z[i] / a_z[0];
     }
     for (i = a_z.Length - 1; i >= 0; i--)
     {
         a_z[i] = a_z[i] / a_z[0];
     }
}

It becomes a bit longer than the one in Butterworth filter because b_z is not just a number but a polynomial here. But that’s now big deal


I initialize ΔΩ with

deltaOmega = dFgap / Math.Sqrt((dFcut - dFgap / 2) * (dFcut + dFgap / 2));

With this implementation order = 2 and a frequency gap of f_h – f_l = 100 Hz at f_c = 500 Hz the filter gets the transfer function

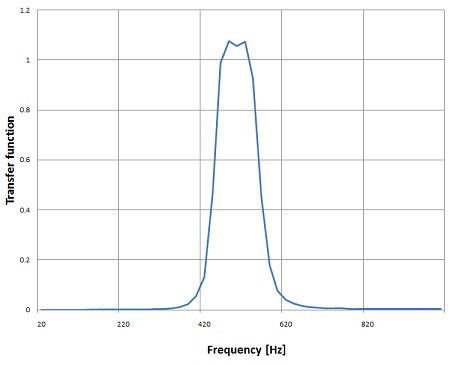
And with a frequency gap of f_h – f_l = 200 Hz at f_c = 500 Hz

It’s quite good visible how much more asymmetrical the transfer function becomes already with the gap of 200 Hz.

The low pass to band stop transformation is similar to a low pass to band pass transformation. In some descriptions they say you have to perform a low pass to high pass transformation first and do a high pass to band stop transformation with the same substitution as done for the low pass to band pass transformation:

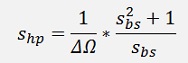
As the low pass to high pass transformation (see Butterworth filter ) is done by the substitution

The low pass to band stop filter transformation can be done by just invert the substitution of the low pass to band pass transformation:

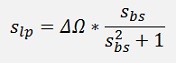
Which means

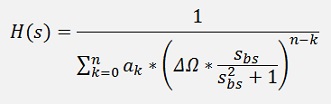
The fraction in the denominator must be eliminated again:

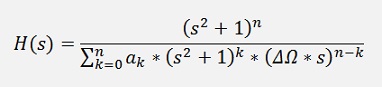
Or in the C# function:

public void BandFilterTransformation()
{
     int i, j;
     double[] tempA = { 1.0 , 0.0, 1.0 }; // s^2 + 1
     double[] tempB = { deltaOmeaga, 0.0 };   // s * deltaQ
    
     List<double[]> bandPar = new List<double[]>();
     for (i = 0; i <= order; i++)
     {
         double[] tempEl = Poly.Mult(Poly.Power(tempA, i), Poly.Power(tempB, order - i));
         tempEl = Poly.Mult(tempEl, a_s[i]);
         bandPar.Insert(i, tempEl);
     }
     Array.Resize(ref  a_s, bandPar.ElementAt(bandPar.Count-1).Length);
     for (i = 0; i < a_s.Length; i++)
     {
         a_s[a_s.Length - 1 - i] = 0;
         for (j = 0; j < bandPar.Count; j++)
         {
              if(i < bandPar.ElementAt(j).Length)
                   a_s[a_s.Length - 1 - i] = a_s[a_s.Length - 1 - i] + bandPar.ElementAt(j)[bandPar.ElementAt(j).Length - 1 - i];
         }
     }
    
     b_s = Poly.Power(tempA,  order);
}

That creates the transfer function

For the order = 3 and a frequency gap of f_h – f_l = 200 Hz at fc = 500 Hz It’s slopes are principally less steep than the ones of the band pass filter. The band pass filter is already quite useful with the order = 2 whereas the band stop is still not too selective at the order = 3 and it shows an awful transient response for higher frequencies.

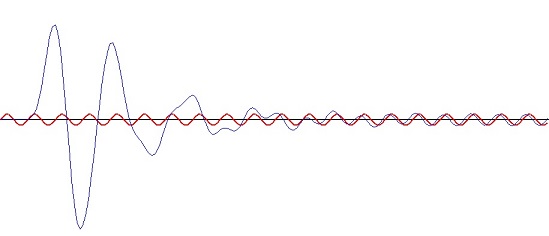
This is the transient response for the same filter at 1000 Hz. It takes 13 cycles to settle. That’s not too nice I think. But that seems to be the way it is

C# Demo Project Butterworth band pass and band stop filter