To solve an definite integral of a continuous function f(x) a simple approach is to compute the parameters of the polynomial interpolation (See Polynomial interpolation) to the function of this integral and to integrate this polynomial. The procedure therefor is to compute some points of the function as the supporting points for the interpolation, compute the polynomial to interpolate these supporting points and build the definite integral for this polynomial.
From the polynomial interpolation we get:
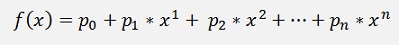
and with this the definite integral becomes

and the integral from a to b
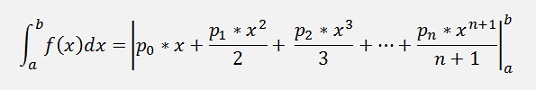
and that’s
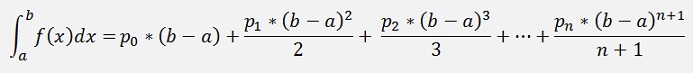
The more supporting points are used the more accurate the integration will become.
I implemented that like:
// fill matrix upside down
for (i = 0; i < order; i++)
{
y[i]
= y_k[order - 1 - i];
for (k = 0; k < order; k++)
{
}for (k = 0; k < order; k++)
{
m[i,
k]
= Math.Pow(x_k[order
- 1 - i], (double)(k));
}if (gauss.Eliminate())
{
gauss.Solve();
integral = 0;
// integration
for (i = 0; i < order; i++)
{
}integral = 0;
// integration
for (i = 0; i < order; i++)
{
integral
= integral + x[i] * (Math.Pow(b,
i + 1) - Math.Pow(a,
i + 1)) / (i + 1);
}else
MessageBox.Show("Matrix calculattion", "Error", MessageBoxButtons.OK,
MessageBoxIcon.Exclamation);
The matrix for the polynomial interpolation is filled upside down to increase the accuracy of the matrix calculations in the Gaussian algorithm (See The elimination algorithm by Gauss).
The supporting points must be placed in the arrays x_k and y_k. From there they are put into the instance m of the matrix class containing an array a of the size n*n, the solution vector y and the vector of the unknowns x.
The result of this sequence is the integral of the function represented in x_k and y_k. It’s put into the variable “integral”.
The disadvantage of this approach is that, depending on the shape of the function, the polynomial interpolation is not too stabile for bigger numbers of supporting points. It can tend to osculate and therefor yield a inaccurate result.
If the graph of the shape to be integrated is a bit more complex, the interpolation by the use of natural splines (See Interpolation by Natural splines) might be the better idea. The spline interpolation tends much less to instability than the polynomial interpolation does. With the natural splines we get one cubic polynomial for each intersection between two supporting points like

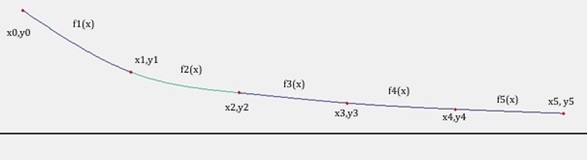
(xi, yi) is one supporting point and the function fi(x) is defined from this supporting point to the next one. That means x runs from xi till xi+1 and so the polynomial runs 0 to xi+1 – xi. Therefore we can make a small substitution:
xp = x-xi
and with this

and the definite integral of this becomes

The starting value a = 0 and b = xi+1 – xi. which is hi in the formulation for the natural splines. That means that:
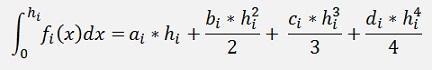
And this formulation is valid for all n-1 intersections between the n supporting points.
In a small c# function that looks like:
public double Integrate(int order)
{
int
i;
double integral = 0;
for (i = 0; i < order - 1; i++)
{
return integral;
}double integral = 0;
for (i = 0; i < order - 1; i++)
{
integral
= integral + (a[i] * h[i] + b[i] * Math.Pow(h[i],
2) / 2.0 + c[i] * Math.Pow(h[i],
3) / 3.0 +
d[i] * Math.Pow(h[i],
4) / 4.0);
}return integral;
But of course the spline parameters a, b, c and d must be computed first and be placed into the corresponding arrays. That’s quite a bit the bigger part of the calculation effort

I found an interesting sample function for a comparison of these two algorithms:

Using the polynomial interpolation I got
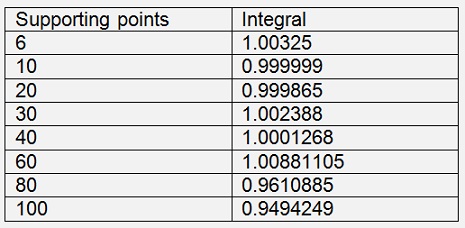
With 100 supporting points the graph is still looking o.k. but the integral is quite inaccurate already.

Using the spline interpolation I got
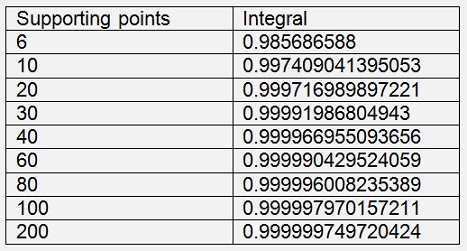
Quite nice


