Carl Runge and Wilhelm Kutta developed a family of methods to solve an ordinary differential equation of the form:
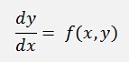
The idea is to calculate y for a random x and therefore the basic formulation for an iterative approximation of y by Runge and Kutta is
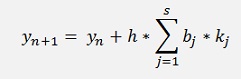
With h = step size and
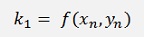
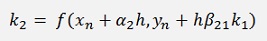
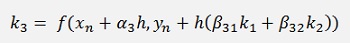
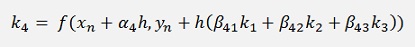
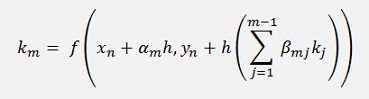
That looks quite complicate but fortunately not all formulations use all numbers of k.
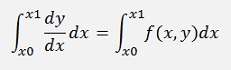
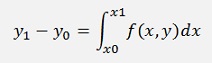
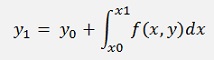
Now the definite integral is solved by the trapezoidal rule
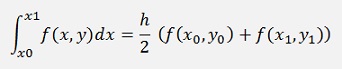
and as the linearization of Euler says
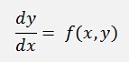
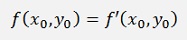
and due to that we can approximate y1 to y1*
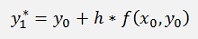
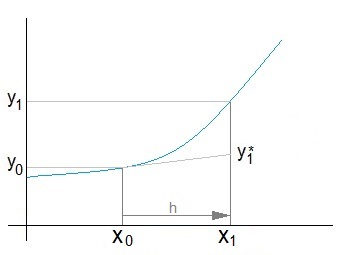
That looks quite inaccurate but with a small step size it’s not too bad

This inserted in the above formula gives:
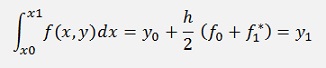
With


That’s the formulation of the Heun algorithm.

is an approximation with the trapezoidal integration rule that uses the trapezoidal

Instead of this we can as well use the function value on the half way from x0 to x1 multiplied by h like

with this we get the formulation of the second order Runge Kutta algorithm:

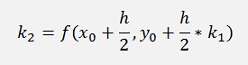
and
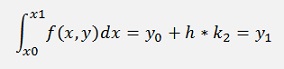
Implemented in a small loop the Heun algorithm looks like:
int i;
double h = 1.0 / (double)(datapoints-1);
double k1, k2;
xp[0] = 0;
yp[0] = 1; // initial value for y[0]
for (i = 1; i < datapoints; i++)
{
xp[i] = i * h;
k1 = f_xy(xp[i - 1], yp[i - 1]);
yp[i] = yp[i - 1] + h/2 * (k1 + f_xy(xp[i], yp[i - 1] + h * k1));
}
For the implementation of the second order Runge Kutta algorithm the last line in the loop must be replaced by the 2 lines
k2 = f_xy(xp[i - 1] + h / 2, yp[i - 1] + h / 2
* k1);
yp[i]
= yp[i - 1] + h * k2;In my sample project I implemented the equation
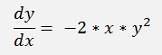
With the initial value y(0) = 1
Which has the exact solution
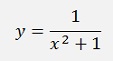
And so
double f_xy(double x, double y)
{
return -2 * x * y * y;
}
With this the exact solution for x = 1 is y = 0.5 The algorithm by Heun returns 0.50000982 and the Runge Kutta approach returns 0.499998 with 100 supporting points.
Similar to the Heun algorithm, the 4. Order Runge Kutta algorithm integrates the main formula
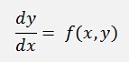
to
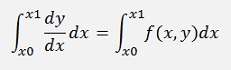
But the definite integral is not solved by the trapezoidal method but the Simpson integral (see Simpson integration for a detailed description)
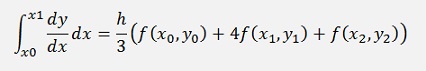

For this approach y1 and y2 must be computed somehow. Therefore y1 is approximated according to Heun as y1* = y0 + h*f(x0). This will be used later on.
With 3 supporting points we can set up a 3. order polynomial to approximate the function f(x) within the interval x0 to x2. That leads to the following 4 equations:
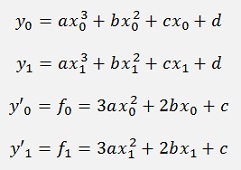
whereas

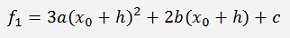
Now the basic approach would be to solve this matrix equation. But that would end in a hell of a calculation.
A more suitable way to proceed is to do a parameter comparison:
At the end we need the solution for the approximation of y2:
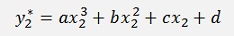
which can be written as:

or expanded:

From this equation a, b, c and d should vanish as they are unknown.
Therefore I first try to get rid of the h3 term in the a part.
If we have a look on a term
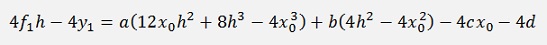
If this is subtracted from the equation for y2*

Some parts already vanished. But there is still 5x03 in the a part. That’s 4 too much. So I subtract 5y0
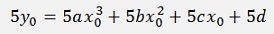

Now it’s easy to see that there is only the subtraction of 2g0h that remains:

and with this
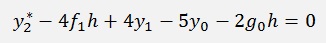
or

and according to Heun
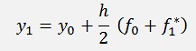
If this is inserted in the above formula we get

Or simplified
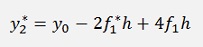
with
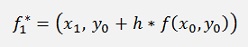
Now everything can be put together in the Simpson formula
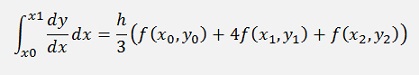
With the approximation for y2 we have
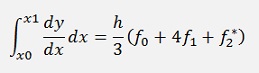
with

Or in the Runge Kutta form
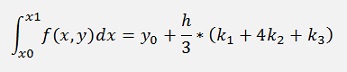
with

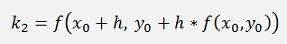
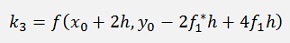
Now there is only one thing the remains: With this formulation h = (x1 – x0)/2. But we need h = (x1 – x0). That means we have to divide every h from above by 2 and get

With
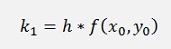

and with
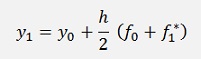
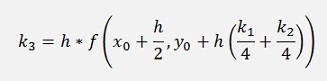
and as


In a small c# sequence that looks like:
double h = 1.0 / (double)(datapoints - 1);
double k1, k2, k3, k4;
xp[0] = 0;
yp[0] = 1; // initial value for y[0]
for (i = 1; i < datapoints; i++)
{
xp[i] = i * h;
k1 = f_xy(xp[i - 1], yp[i - 1]);
k2 = f_xy(xp[i - 1] + h / 2, yp[i - 1] + h * k1 / 2);
k3 = f_xy(xp[i - 1] + h / 2, yp[i - 1] + h * (k1 + k2) / 4);
k4 = f_xy(xp[i - 1] + h, yp[i - 1] + h * (-k2 + 2 * k3));
yp[i] = yp[i - 1] + h / 6 * (k1 + 4 * k3 + k4);
}
That looks quite similar to the second order Runge Kutta algorithm. But a comparision of the two’s shows the difference:

With its polynomial approximation the fourth order Runge Kutta algorithm is already quite accurate with just a few data points or a rather big step width between two data points. That makes it quite attractive as it is not too much more complicate to be implemented than the other two’s


