In machine learning we often face the problem of too high complexity together with big amounts of data. If there are many input parameters in a Gradient Descent calculation, the calculation process becomes quite time consuming.
The Principal components analysis is an approach to reduce the number of input parameters without losing too much of information. That can reduce the calculation effort quite a bit.
An origin data set with a 4 dimensional input like:
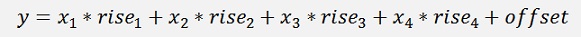
Shall be reduced to a data set of less dimensions. A reduction to 2 dimensions would be:
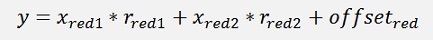
An approximation of this data set by a gradient descend algorithm consumes much less calculation effort than the computation of the origin data set. That makes the principal component analysis quite interesting in the field of artificial intelligence.
For a given set of data points the Principal components analysis basically rotates the coordinate system to get the biggest variation in the first axis (and smaller variations in the other axes)
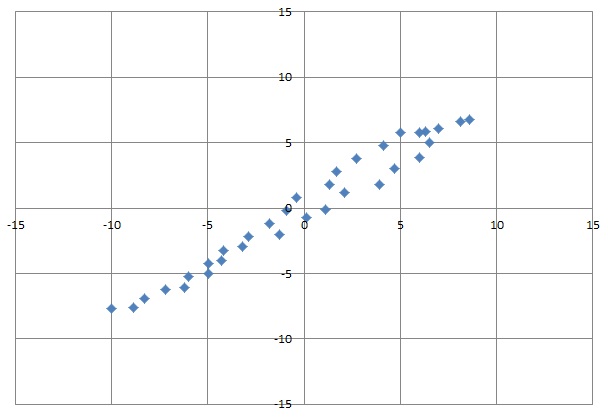
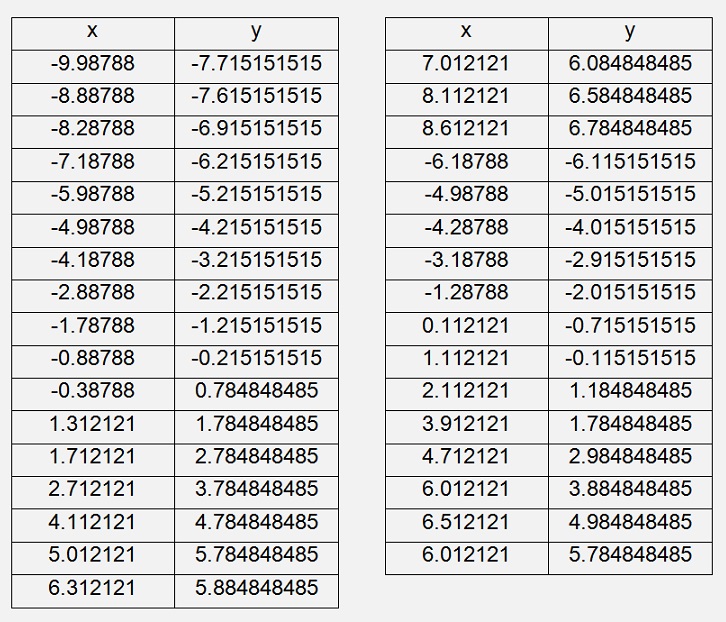
For a normalised 2 dimensional data set like:
That would be
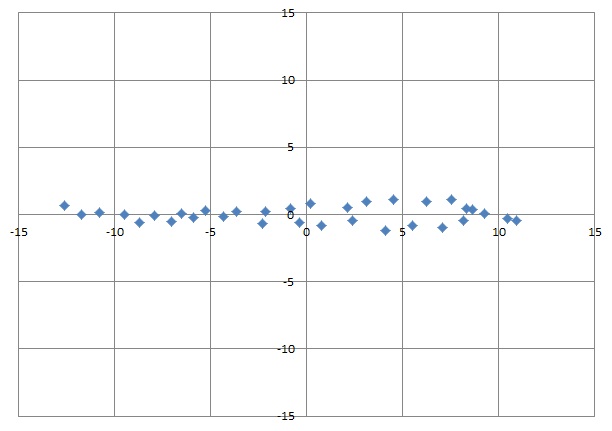
After this rotation the biggest variation is on the horizontal axis and a very small variation on the vertical axis.
Without this rotation we have almost the same variation on both axes. But now we can see that we got a very small variation of something around -1.1 to +1.1 on the vertical axis whereas on the horizontal we got -13 to +11. With this information we can neglect the variation of the vertical dimension and reduce this data set to a 1 dimensional set. With this reduced data set we can perform a Gradient Descent calculation with much less effort and know, we will not lose too much information.
But one important point must be considered: At the end of the Gradient Descent calculation we get a result that does not have too much to do with origin 2 dimensional input data set. We will have to rotate the coordinate system back to its origin first, or the input data must be rotated each time before it is computed. But more to this later

To deduce the math behind this algorithm there are some definitions to be made:
- The transformation of the data shall be made by a matrix multiplication.
- The used matrix shall be orthonormal.
- The backward transformation shall lead to smallest deviations in square.
With these definitions let the transformation function be f(x) = xreduced. Whereas x is a vector of n dimensions and xreduced is the reduced vector. The function for the backward transformation shall be the matrix multiplication g(xreduced) = D* xreduced. With D as the transformation matrix.
Now the formulation for the deviations of the backward transformation is:
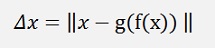
or
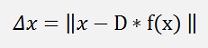
and that shall be minimized.
As x and D*f(x) both are vectors this formulation can be written as:
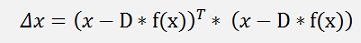
this can be expanded to:
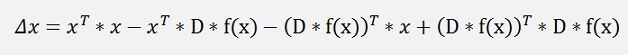
and as
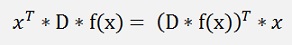
(see Transposed Matrix)
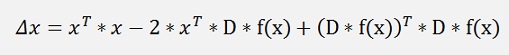
with
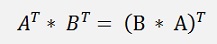
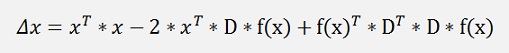
and as D is orthonormal
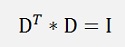
and
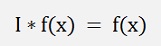
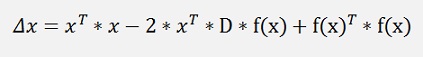
Finally we can say xT * x is not variable regarding the minimum search and can be neglected.
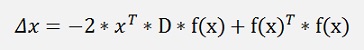
To find the minimum of this the gradient of this formulation must be 0.
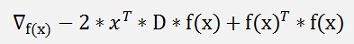
And that is the case if

(As f(x) shall be a matrix multiplication f(x)T + f(x) = (f(x)2)T)
Or the entire formula transposed:
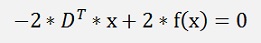
and so
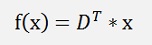
That means the minimum of Δx is where f(x) = DT * x. The transformation is done by the multiplication of x by D transposed. The backward transformation is done as defined further above by multiplication of the reduced data set xreduced by D.
This is the bare formulation for the transformation.
Now we have to find the type of D.
With this the formulation for the deviation can be written as
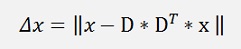
For the deduction we just look at the case of a reduction to one column and reduce D to its first column vector d
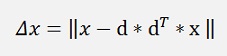
and as dT * x is a single number, we can switch
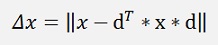
and switch dT * x to xT * d
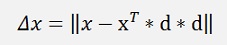
This is the formulation for one x-vector. If we include the entire data set X now. Therefore we first have to write this formulation to get one row of X (instead of column vectors) d
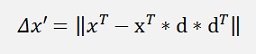
And now xT can be replace by X
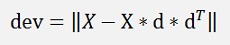
That yields the deviation for the entire data set. This again can be written as
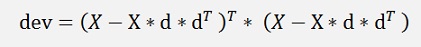
or
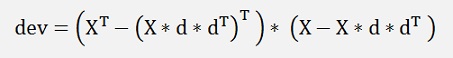
This can be expanded to
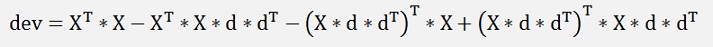
With
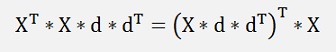
We get
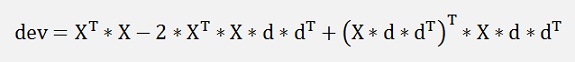
or
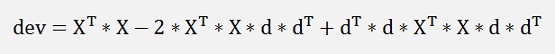
and as D is orthonormal therefore and dT * d = 1
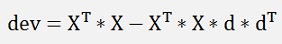
this shall be minimized by d now and as XT * X does not influence that, it can be neglected and we get:
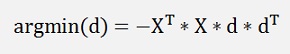
and that’s equal to
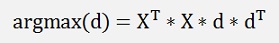
this multiplied by another d removed dT on the right side gives:
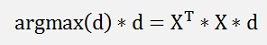
That’s the equation of a Eigenvector d and its Eigenvalue which is the expression argmax(d). We are looking for the biggest Eigenvalue and its Eigenvector and the multiplication of this transposed Eigenvector d by X will create the smallest deviation between the approximated values and the origin values.
For the next smaller Eigenvalue and Eigenvector of the same matrix the deviation to the origin data will be bigger. For the following one it will be even bigger and so on. If all Eigenvectors are computed and put into a matrix D with Eigenvalues ordered descending from left to the right, we have a rotation matrix that rotates the origin data X the way that we get a new matrix of the same size as X that has in the first column a factor that creates the smallest deviation, in the second row, orthogonal to the first, the second smallest deviation and so on. In the last row there is a factor that has the biggest deviation. That means this last column has the least impact on the accuracy of the approximated data. This column can be neglected without losing too much of information. Basically the rows with small Eigenvalues can be neglected.
That’s the way a computer program can find out which columns can be neglected.
In the literature there is often the covariance matrix of X mentioned to compute the Eigenvalues. The covariance matrix is a matrix that contains the information about all kinds of deviations of a data set. For a data set x1 … xk with N samples its elements are defined as
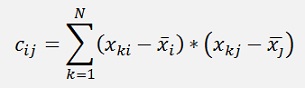
If the data set is normalised the way that the mean of each column is 0, the covariance matrix becomes:

And so the Eigenvalues and vectors are computed from this. In the same literature there is mentioned that the input data must be normalized the way that the mean of each column is 0.Purely mathematical I regard it as wrong to use the covariance matrix. But as the data is normalized in most cases it basically works and if a library is used to compute, it’s a convenient solution

For the 2 dimensional data set from above:
The XT * X matrix is
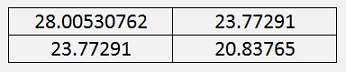
An important detail is the fact that this matrix is symmetric to the main diagonal. This is always the case and lets the Eigenvalues to be computed by the Jacobi algorithm (see Eigenvalues of a symmetric matrix by Jacobi)
The Eigenvector matrix of this is.

This is a rotation matrix that rotates by 40.7°(see Rotation Matrix) If you compare that with the graphic on top of this article, that fits perfect.
In a 2 dimensional matrix the rotation can be seen easily. In a matrix of higher order it might be a bit more hidden

The Eigenvalues of the same matrix are:

We were looking for the biggest Eigenvalue. That’s the first one. The second one is much smaller. That means the second column of our rotated data has a very small impact on the information (as we already saw in the graphic) and can be neglected.
After transformation the data set looks like:
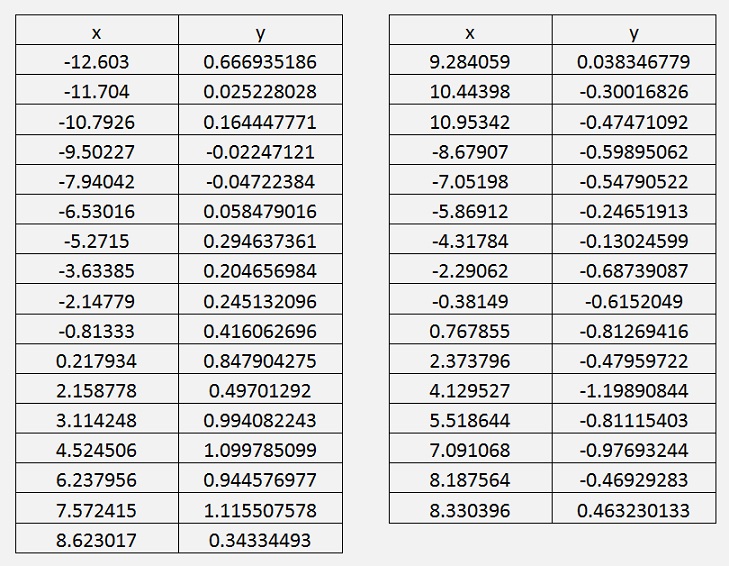
Garient descend with reduced data
O.k. a 2 dimensional data set is possibly not too interesting to apply this data reduction. But it is quite a good sample to understand the maths behind it. In my sample application I started with data set with 4 dimensions and compare the result with my gradient descend algorithm (see Gradient descend) . I reduce the data by 2 dimensions and perform the same gradient descend algorithm for comparison.
But first some words to the algorithm:
I use 2 constants to define the number of features:
const int features = 4;// number of features (or dimensions) of the input data
const int redfeatures = 2; // number of features (or dimensions) of the reduced data
The number of the input features should be equal to the number features read from the data file data.csv. This must be checked. The number of reduced features can be set free. O.k. it should not be bigger than features (would not make sense) and I would not set it too small. It’s a matter of accuracy. The smaller the number of reduced features the smaller the accuracy of the final approximation will be.
For the data handling I implemented the class Data. This class handles the reading of the input data from the .csv file, the normalization and keeps the mean values and the deviations of the input data. The normalization is done for each column separately and a mean value and deviation is kept for the revers transformation at the end. For the computation of the Eigenvalues and Eigenvectors I use my “Jacobi” algorithm as mentioned. It’s in the class Jacobi. It takes the input in the matrix a, puts the Eigenvectors in the matrix v and has the Eigenvalues in the main diagonal of a after finishing.
So the computation procedure starts with:
data.calcMean(features);
data.normalize(features);
for (i = 0; i < features; i++)
{
for (j = 0; j < features; j++)
{
jacobi.a[i, j] = CalcXTX(data.values, i, j);
}
}
jacobi.RunJacobi();
calc_rotation_matrix(features - redfeatures);
with
void calc_rotation_matrix(int nbOfMins)
{
int i, j, k;
double actMinVal = -1E20;
double tempMinVal = 1E20;
int indexOfMin = -1;
int actIndex = 0;
for (k = 0; k < nbOfMins; k++)
{
tempMinVal = 1E20;
for (i = 0; i < features; i++)
{
if ((Math.Abs(jacobi.a[i, i]) < tempMinVal) &&(Math.Abs(jacobi.a[i, i]) > actMinVal))
{
tempMinVal = Math.Abs(jacobi.a[i, i]);
indexOfMin = i;
}
}
actMinVal = tempMinVal;
}
for (i = 0; i < features; i++)
{
if (Math.Abs(jacobi.a[i, i]) > actMinVal)
{
for (j = 0; j < features; j++)
{
convMatrix[j, actIndex] = jacobi.v[j, i];
}
actIndex++;
}
}
}
In the function calc_rotation_matrix I don’t use all the Eigenvectors for the rotation matrix. It is enough just to take the Eigenvectors for the columns I use. I look for the features – redfeatures number of minimum Eigenvalues, put this in actMinVal and take only the Eigenvectors that have bigger Eigenvalues than the actMinVal. That reduces the calculation effort a bit. At the end of this function I have the rotation matrix in convMatrix.
With this convMatrix I compute the reduced data set with:
double[] tempVals;
for (k = 0; k < samples; k++)
{
double[] reducedLine = new double[redfeatures + 1];
tempVals = data.values.ElementAt(k);
for (i = 0; i < redfeatures; i++)
{
reducedLine[i] = 0;
for (j = 0; j < features; j++)
reducedLine[i] = reducedLine[i] + tempVals[j] * convMatrix[j, i];
}
reducedLine[redfeatures] = tempVals[features];
reducedValues.Add(reducedLine);
}
That puts the new data into the list reducedValues. With this list I start the gradient descend computation now. Therefor I use the same algorithm I already used in my Gradient descend algorithm. I just switch the input data to the reducedValues list and use the const redfeatures instead of features.
With the computed result there are 2 options now. We can use the values as they are. But in this case the input data has to be normalized and rotated before it can be processed. The second option is to make a backward conversation of the rise and offset values and use this converted values for the later data processing.
The main window of my sample project looks like:
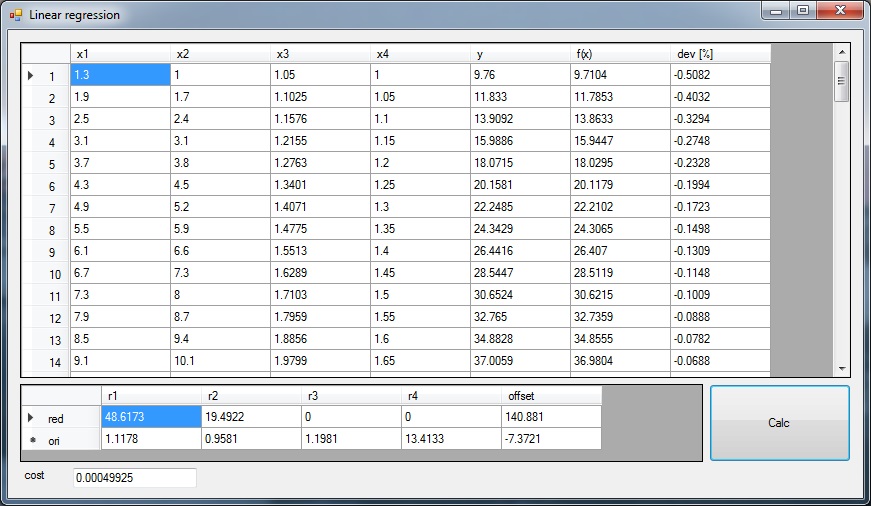
In the upper data grid there is the origin input data in the first 5 columns. In the 6. column is the approximated y value. For this approximation I use the reduced data to compute. In the last column there is the difference between the origin y value and the approximated one in %.
In the lower data grid there are the computed rise and offset values of the reduced input data in the upper row and the backward converted rise and offset values in the lower row. In the project directory there is an Excel sheet containing the origin data and for comparison the approximated y values by the use of the backward transformed rise and offset values. Just in case somebody is interested in that

For the backward transformation we have to make a parameter comparison:
The origin formulation is:
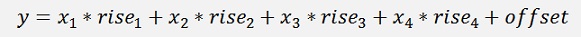
For the normalised, reduced data we have:
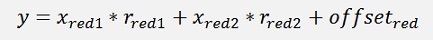
with
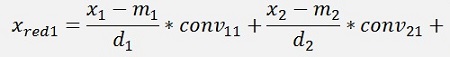
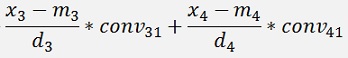
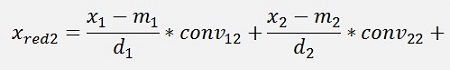
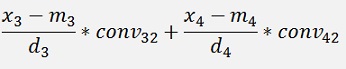
with
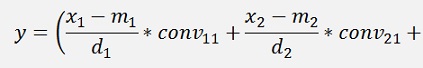
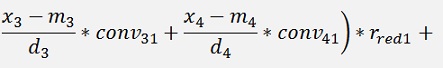
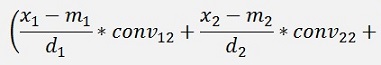
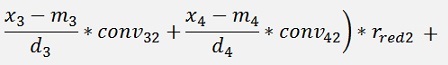
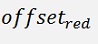
with convij as the elements of the convMatrix matrix.
As the mean mkl values are independent on the x values we can write:
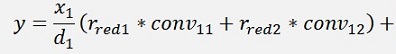
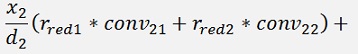
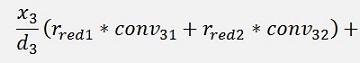
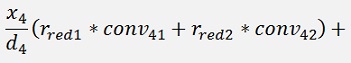
and
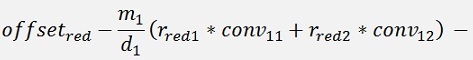
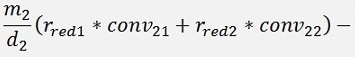
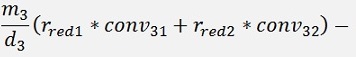
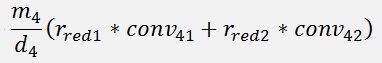
In code that’s the following function:
void Calc_invers_rotation()
{
int i, j;
offset_ori = offset;
for (i = 0; i < features; i++)
{
rise_ori[i] = 0;
for (j = 0; j < redfeatures; j++)
{
rise_ori[i] = rise_ori[i] + rise[j] * convMatrix[i, j];
offset_ori = offset_ori - (data.mean[i] / data.deviation[i] * rise[j] * convMatrix[i, j]);
}
rise_ori[i] = rise_ori[i] / data.deviation[i];
}
}
In numbers I get for the reduced data

This rotated backward and “not normalised” is:

The gradient descend algorithm with the origin data set without reduction get’s

The origin data I built with:

That looks all quite far away from each other. But, as I already mentioned in Gradient descend, the approximation is only valid for data that is within the scope of the sample data and there it is quit o.k. for all 3 versions:
A comparison of the deviations between the origin data and the approximated shows

O.k. with the origin data set the result is really more accurate. But this calculation takes a bit more time.
The computation of the full data set takes between 1.6 and 2 seconds whereas the reduced data set takes 08 to 0.9 seconds. That’s almost half as long

Excel sheet to Principal components analysis 2 dimensional iterative

